61：单选、

1/42+1/56+1/72+1/90+1/110的值是（    ）。

A 41645

B 5/66

C 7/85

D 11/128

【答案】B

【解析】解法一：1/42+1/56+1/72+1/90+1/110=1/6-1/7+1/7-1/8+1/8-1/9+1/9-1/10+1/10-1/11=1/6-1/11=5/66因此，答案选择B选项。。

【技巧】裂项相加法

【拓展】裂项相加公式： 

62：单选、

在自然数1至50中，将所有不能被3除尽的数相加，所得的和是（    ）。

A 865

B 866

C 867

D 868

【答案】C

【解析】解法一：1～50所有数字的和为（1+50）×50/2=1275，1～50能被3整除的数字和为（3+48）×16/2=408，因此将所有不能被3除尽的数相加，和为1275-408=867。解法二：不能被3除尽的数字有两类：从1开始公差为3，最后项为49，共17项，和为17*（1+49）/2=425，从2开始公差为3，最后项为50，共17项,和为17*(2+50)/2=442，总和为867。因此，答案选择C选项。

【技巧】公式法

63：单选、

一个边长为1的正方形木板，锯掉四个角使其变成正八边形，那么正八边形的边长是多少？（    ）

A 12

B 22

C 2- 

D  -1

【答案】D

【解析】设正八边形边长为x,那么被截掉的小三角直角边长就是x/ 。因为原先正方形边长为1，所以x+ x=1,解得x=1/（1+ ）= -1，因此，答案选择D选项。

【技巧】方程法

64：单选、

A 15°

B 20°

C 25°

D 30°

【答案】A

【解析】解法一：AB=AC，则∠ABC=∠ACB；AM=AN，则∠AMN=∠ANM。又∠ANC=∠BAN+∠ABN=30°+∠ACB，∠ANC=∠ANM+∠CNM=∠AMN+∠CNM=∠CNM+∠MCN+∠CNM=2∠CNM+∠MCN=30°+∠ACB；所以2∠CNM=30°，∠CNM=15°。解法二：特殊值法：作为三角形的正三角形也应满足题意。如下图，从图中易求得∠ANM=15°。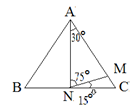 因此，本题选择A选项。

【技巧】赋值法