141：单选、

在一次法律知识竞赛中，甲机关20人参加竞赛，平均分是80分，乙机关30人参加竞赛，平均分是70分，请问两个机关参加竞赛的人的平均分是多少？

A 76分

B 75分

C 74分

D 73分

【答案】C

【解析】根据平均数的定义两个机关参加竞赛的人的平均分= =74。因此，本题答案为C选项。

【技巧】公式法

142：单选、

一单位组织员工乘坐旅游车去泰山，要求每辆车上的员工人数相等。起初，每辆车上坐22人，结果有1人无法上车；如果开车走一辆空车，那么所有的旅游者正好能平均乘到其余各辆旅游车上，已知每辆车上最多能乘坐32人。请问该单位共有多少员工去了泰山？

A 269人

B 352人

C 478人

D 529人

【答案】D

【解析】设车的数量为x，则总人数为22x+1是一个奇数，排除BC，又因为车的数量必须是一个整数，即总人数减去1后能够整除22，即既能被2整除也能被11整除，代入可知D正确。因此，本题答案为D选项。

【技巧】奇偶特性，倍数特性法

143：单选、

某市一体育场有三条同心圆的跑道，里圈跑道长1/5公里，中圈跑道长1/4公里，外圈跑道3/8公里。甲、乙、丙三人分别在里、中、外圈同一起跑线同时同向跑步。甲每小时跑3.5公里，乙每小时跑4公里，丙每小时5公里，问几小时后三人同时回到出发点？

A 8小时

B 7小时

C 6小时

D 5小时

【答案】C

【解析】甲跑一圈所需的时间是1/5÷3.5=2/35，乙跑一圈所需的时间是1/4÷4=1/16，丙跑一圈所需的时间是3/8÷5=3/40，三人同时回到出发点所需的时间就是2/35，1/16，3/40的最小公倍数即为6。因此，本题答案为C选项。解法二：甲跑一圈所需的时间是1/5÷3.5=2/35，丙跑一圈所需的时间是3/8÷5=3/40，所以时间能被2和3整除，结合选项可知C正确。因此，本题答案为C选项。

【释义】分数最小公倍数的求法：用各分子的最小公倍数作分子，各分母的最大公约数作分母，所得分数就是各分数的最小公倍数。

【技巧】倍数特性法

144：单选、

某单位的员工不足50人，在参加全市组织的一次业务知识考试中全单位有1/7的人得90-100分，有1/2的人得80-89分，有1/3的人得60-79分。请问这个单位得60分（不含60分）以下考试成绩的有多少人？

A 1人

B 2人

C 3人

D 4人

【答案】A

【解析】由题意可知，总人数能同时被7，2，3整除，也就是能被42整除，因为人数少于50，所以人数就只能是42人，得90-100分的为42× =6人，得80-89分的为42× 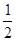=21人，得60-79分的为42× 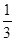=14人，所以这个单位得60分（不含60分）以下考试成绩的有42-7-21-14=1人。因此，本题答案为A选项。

【技巧】倍数特性法