25：单选题、

下图是一个奥林匹克五环标识。这五个环相交成9部分A、B、C、D、E、F、G、H、I。请将数字1、2、3、4、5、6、7、8、9分别填入这9个部分中，使得五环内的数字之和恰好构成五个连续的自然数。那么，这五个连续自然数和的最大值是多少？（    ）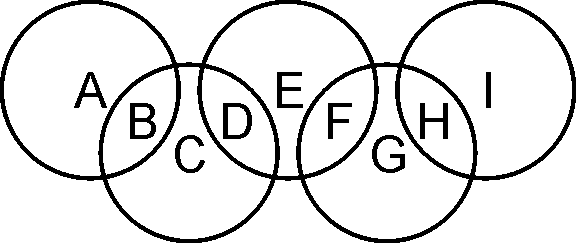

A 65

B 75

C 70

D 102

【答案】C

【解析】因为B、D、F、H同时出现在两个圆圈中而其他数都出现在一个圆圈中，所以五个圆圈中的总和为1＋2＋3＋……＋9＋B＋D＋F＋H≤45＋9＋8＋7＋6＝75。若五个圆圈中的总和为75，则B＋D＋F＋H＝9＋8＋7＋6＝30，又因为五个环内的数字和恰好构成五个连续的自然数，所以这五个环内的数字只能是13、14、15、16、17，考虑两端两个圆圈中的总和，S＝（A＋B）＋（H＋I）≥13＋14＝27，但B＋H≤9＋8＝17，A＋I≤4＋5＝9，所以S最大为26，与上面的结论矛盾，所以五个圆圈中的总和不可能为75，又因为五个连续自然数的和是5的倍数，所以五个圆圈中的总和最大为70。当（A、B、C、D、E、F、G、H、I）＝（9、7、3、4、2、6、1、8、5）时，五个圆圈的总和就可以取到70，故正确答案为C。

26：单选题、

下图中的大正方形ABCD的面积是1平方厘米，其他点都是它所在边的中点。那么，阴影三角形的面积是多少平方厘米？（    ）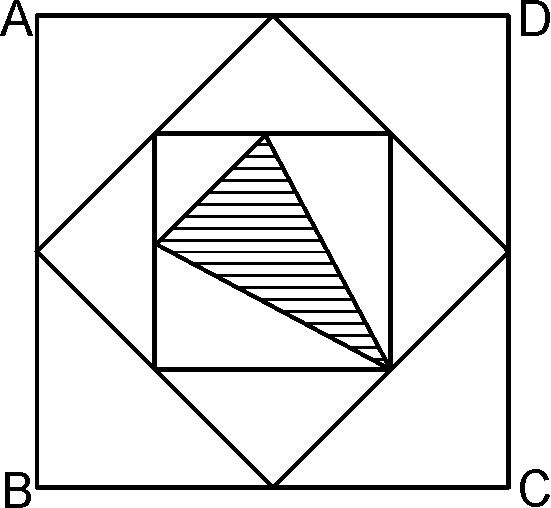

A 42152

B 7/34

C 3/32

D 5/38

【答案】C

【解析】C连接正方形4个中点得到的小正方形的面积是大正方形的1/2，因为连接小正方形的对角线，这两条对角线把大正方形分成相等4部分，每部分的一半一起构成了小正方形。因此，中间的最小正方形的面积是1/4.求阴影部分的面积，可以求出最小正方形中非阴影部分，容易得出为最小正方形的5/8.所以阴影部分为最小正方形的3/8，（3/8）x（1/4）=3/32.本题答案为C选项。

27：单选题、

把自然数按由小到大的顺序排列起来组成第一串数：1、2、3、…、9、10、11、12、…，把这串数中两位以上的数全部隔开成一位数字，组成第二串数：1、2、…、9、1、1、1、2、1、3、…。则第一串数中100的个位数字0在第二串数中是第几个数？（    ）

A 188

B 198

C 192

D 202

【答案】C

【解析】第二串数一位数有9个，两位数（10～99）有90个，所以第一串数中100的个位数字0在第二串数字中的位置是9+90×2+3＝192个。因此，本题答案为C选项。

28：单选题、

数学竞赛团体奖的奖品是10000本数学课外读物。奖品发给前五名代表队所在的学校。名次在前的代表队获奖的本数多，且每一名次的奖品本数都是100的整数倍。如果第一名所得的本数是第二名与第三名所得的本数之和，第二名所得的本数是第四名与第五名所得本数之和。那么，第三名最多可以获得多少本？（    ）

A 1600

B 1800

C 1700

D 2100

【答案】C

【解析】假设一到五名获得的本数分别为：a，b，c，d，e。则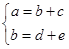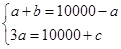： ， ，因为每一名次的奖品本数是100的整数倍，故10000+c必须能被3整除。因此，本题答案为C选项。