57：单选题、

一个四边形广场，它的四边长分别是60米、72米、96米、84米，现在四边上植树，四角需种树，而且每两棵树的间隔相等，那么，至少要种多少棵树？（    ）

A 22

B 25

C 26

D 30

【答案】C

【解析】若要四个角均种树，树的间隔必须为四个边的约数，也就是60、72、96、84的公约数，求“至少要种多少棵树”，也就意味着树的间隔最大，所以，本题核心是求60、72、96、84的最大公约数，最大公约数为12，所以至少要种树 棵树，因此，本题答案为C选项。

【拓展】典型的求最大公约数题型，另外长方形纸张撕成若干正方形的题目，是另一典型最大公约数题型。

58：单选题、

甲、乙二人同时同地绕400米的环形跑道同向而行，甲每秒钟跑8米，乙每秒钟跑9米，多少秒后甲、乙二人第三次相遇？（）

A 400

B 800

C 1200

D 1600

【答案】C

【解析】甲乙速度方向相同，为追及问题，相遇一次，意味着甲乙路程之差为一圈即400米，相遇第三次，意味着甲乙路程之差为3圈，即1200米，所以所求为 秒，因此，本题答案为C选项。

59：单选题、

一个等腰三角形，两边长分别为5cm、2cm，则周长为多少cm？（    ）

A 12

B 9

C 12或9

D 无法确定

【答案】A

【解析】根据三角形三边关系，三角形两边之和大于第三边，所以三角形的腰只能是5cm，因此周长为 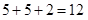cm，因此，本题答案为A选项。

【拓展】本题只是求周长，用到了三角形三边关系，考试中，还会遇到给了最大边长求组成多少个三角形的题目，三角形三边关系仍然是考点之一。

60：单选题、

电影票10元一张，降价后观众增加一倍，收入增加1/5，则一张票降价多少元？（    ）

A 8

B 6

C 4

D 2

【答案】C

【解析】假设原有观众2人，降价后观众就为4人，设后来的票价为 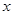元/张，根据题意，可以列方程： ，解得 ，所以降价 元，因此，本题答案为C选项。

【技巧】赋值法