69：单选题、

1，（    ），1/7，1/13，1/21

B 1

C 42006

D 42007

【答案】D

【解析】把原数列化为：1/1，（    ），1/7，1/13，1/21。分母分别为1，（    ），7，13，21。后三项依次差6，8，猜测是二级等差数列：2，4，6，8，则空缺项分母应为3，验证成立。因此，本题答案为D选项。

70：单选题、

［（9，6），42，（7，7）］［（7，3），40，（5，5）］［（8，2），（    ），（3，2）］

A 30

B 32

C 34

D 36

【答案】A

【解析】每组中中间项＝前两项的差×后两项的和。第一组：42=（9-6）×（7+7）；第二组：40＝（7－3）×（5＋5）；第三组：（）=（8-2）×（3+2）=30。因此，本题答案为A选项。

【纠错】有同学仅看每组数列的中间数字：42=6×7；40=5×8；（    ）=4×9=36，误选答案D选项。而这种做法，仅靠2个数字就推第三个数字是不可靠的，并且也没有用到每组内的其他数字，因此是错误的。

71：单选题、

2009×20082008－2008×20092009＝？（    ）

B 1

C 2

D 3

【答案】A

【解析】解法一：尾数法。2009×20082008的尾数为2，2008×20092009的尾数也为2，两者相减的尾数必为0。因此，本题答案为A选项。解法二：因式分解法。原式=2009×2008×10001-2008×2009×10001=0。因此，本题答案为A选项。

【技巧】尾数法、因式分解法

72：单选题、

在1~101中5的倍数的所有数的平均数是（    ）

A 52.5

B 53.5

C 54.5

D 55.5

【答案】A

【解析】解法一：1~101中5的倍数分别为5、10、15……100，这串数列是以公差为5的等差数列。根据等差数列的性质，平均数=中位数。数列20项，中间两项分别是第10项、第11项， =5+100=105，则中位数为52.5，即平均数也是52.5。因此，本题答案为A选项。解法二：1~101中5的倍数分别为5、10、15……100，这串数列是以公差为5的等差数列。根据等差数列求和公式， （首项+末项）×项数，则平均数= = 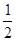（首项+末项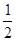）= ×（5+100）=52.5。因此，本题答案为A选项。

【技巧】公式法