29：单选题、

一项工程，甲、乙合作16天完成，乙、丙合作12天完成，丙、丁合作16天完成，如果甲、丁合作完成需要这项工程需要多少天（    ）

A 21

B 24

C 26

D 27

【答案】B

【解析】假设工程总量为题中时间的最小公倍数48，根据题意可得各自效率满足：甲+乙=3①；乙+丙=4②；丙+丁=3③，再用式子①+③-②得：甲+丁=3+3-4=2。所以甲、丁合作完成这项工程需要的天数是48÷2=24。因此，本题答案选择B选项。

【技巧】赋值法、方程法

30：单选题、

某人购买A、B两种调料的单价分别为20元/千克、30元/千克。假设购买这两种调料所花费的钱数额一样，则由A、B两种调料混合后的新调料每千克的成本是（    ）

A 23元

B 24元

C 25元

D 26元

【答案】B

【解析】解法一：设购买这两种调料都花费60元，则两种调料购买的重量分别为3千克、2千克，那么新调料成本为120/（3+2）=24元。因此，本题答案选择B选项。解法二：根据调和平均数公式直接计算，新调料成本为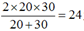元。因此，本题答案选择B选项。

【技巧】赋值法、公式法

31：单选题、

甲、乙两人分别从A、B两地同时出发，相向而行，匀速前进。如果每个人按一定的速度前进，4小时相遇；如果各自每小时比原计划少走1千米，5小时相遇。则AB两地的距离是（    ）

A 40千米

B 20千米

C 30千米

D 10千米

【答案】A

【解析】设AB两地的距离是S，根据题意，可列方程组：S=（v甲+v乙）×4，S=（v甲-1+v乙-1）×5，得v甲+v乙=10，S=40，所以AB两地的距离是40千米。因此，本题答案选择A选项。

【技巧】方程法

32：单选题、

局长找甲、乙、丙三位处长谈话，计划与甲交谈10分钟，与乙交谈12分钟，与丙交谈8分钟。办公室助理通过合理调整三人交谈的顺序，使得三人交谈和等待的总时间最少。请问调整后的总时间为多少？（    ）

A 46分钟

B 48分钟

C 50分钟

D 56分钟

【答案】D

【解析】要使三人交谈的等待总时间最少，则谈话时间短的尽量优先谈，所以应按照丙、甲、乙的顺序谈话，总时长为8+（8+10）+（8+10+12）=56分钟。因此，本题答案选择D选项。