21：单选题、

如下图所示，正方形ABCD的边长是14厘米，其中，BE=CE=7厘米。如果点P以每秒2厘米的速度沿着边线CD从点C出发到点D，那么三角形AEP的面积将以每秒（）平方厘米的速度增加。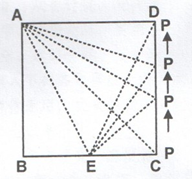

A 7

B 8

C 9

D 10

【答案】A

【解析】三角形AEC经过7秒后变为三角形ADE；三角形AEC的面积=数列首项=a1=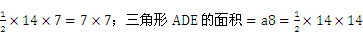；则两者的公差d=（a8-a1）/7=7。因此，本题答案选择A选项。

【技巧】枚举归纳法

22：单选题、

一块合金净重200克，用线吊住全部浸没在水里称重为180克。已知合金包含甲、乙两种金属，由于浮力的作用甲金属在水里减轻 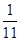的重量，乙金属在水中减轻 的重量。则此块合金中包含的甲乙金属重量相差（）克。

A 10

B 20

C 30

D 40

【答案】B

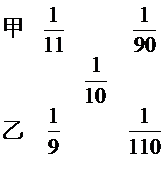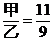【解析】解乏一：甲金属在水里减轻 1/11 的重量，则甲为11的倍数，同理乙为9的倍数，所以，甲=110、乙=90，代入验证符合条件，所以相差110-90=20克。因此，本题答案选择B选项。解法二：由题意，合金在水中减轻1/10，利用十字交叉法则可得，则，相差=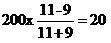。因此，本题答案选择B选项。

【技巧】倍数特性法、代入排除法

23：单选题、

五个各不相等的自然数分别两两相加，10种相加组合共得到8个不同的结果，分别是17、22、25、28、31、33、36与39，则五个数中最大的数与最小的数之和为（）。

A 25

B 28

C 31

D 33

【答案】B

【解析】设五个自然数为a＜b＜c＜d＜e，则可以得到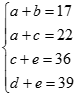，(2a+b+2c+d+2e)=114，则a+c＜b+d＜c+e，所以b+d的大小一定介于22和36之间，b+d＝114-2(a+c+e)，b+d一定是偶数，所以b+d=28，所以a+e＝17＋39－28=28。因此，本题答案选择B选项。

【技巧】整体思维法

24：单选题、

李明倡导低碳出行，每天骑自行车上下班，如果他每小时的车速比原来快3千米，他上班的在途时间只需原来时间的 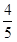；如果他每小时的车速比原来慢3千米，那么他上班的在途时间就比原来的时间多（）。

A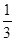  

B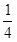  

C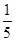  

D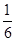  

【答案】A

【解析】设速度为v，又因为，他上班的在途时间只需原来时间的 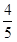，所以赋值原来的时间为5，则加速后的时间为4，S=5v=4（v+3），可得v=12，S=60；减速后的速度为12-3=9，时间为60/9，则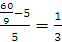。因此，本题答案选择A选项。

【技巧】赋值法、方程法