41：单选题、

某单位举办象棋比赛,规则为胜一场得4分，负一场得-1分，平一场不得分。一轮比赛中参赛人员共100人，两两配对后分別比赛，所有人的总得分为126分，问该轮比赛中平局有多少场？（    ）

A 4

B 8

C 12

D 16

【答案】B

【解析】比赛问题。两两配对比赛，根据题意，要么比赛两队得分和为3分，要么得分和为0（平局）。所有人得分为126分，126/3=42，即共有42场比赛决出胜负，100个人共组成50场比赛，那么有8场为平局，故答案选择B。

【技巧】平均思维

42：单选题、

有甲乙两个水池，其中甲水池中一直有水注入，如果分别安排8台抽水机去抽空甲和乙水池，则分别需要16小时和4小时,如给甲水池加5台，则可以提前10小时抽空。若共安排20台抽水机，则为了保证两个水池能同时抽空，在甲水池工作的抽水机应该比乙水池多多少台？（）

A 4

B 6

C 8

D 10

【答案】C

【解析】方法一：乙的水量是可以算出来的。具体解法为：1）先算甲的进水速度：设出水速度为1，则有（8*16-13*6）/（16-6）=5。所以甲的水量有：16*8-5*16=48。2）然后算乙的水量。因为乙是没有水注入的，所以乙的进水速度为0.出水速度还是1.则水量=4*8*1=32。3）最后我们需要设一个方程，设甲的抽水机x，乙的为y,用时为t。有x+y=20，48=（1*x-5）*t，32=y*t。联立三个方程，可得x=14,y=6。所以答案为C。方法二：根据题意，当用甲水池用8台抽水机用时16小时可以抽完，乙水池8台抽水机用时4小时可以抽完。当甲水池13台抽水机用时6小时可以完成。现在是20台抽水机，如果相差是4，则甲水池是12、乙水池是8，很明显甲水池在4小时抽不完，排除;如果相差是6，则甲水池的是13，乙水池的是7，甲水池用时6小时完成，乙水池用时8×4/7，很明显不是6，排除;如果相差8，那么甲水池的是14，乙水池的是6，这个计算比较麻烦，先看下面的选项;如果相差10，那么甲水池就是15，乙水池就是5，很明显甲水池的在6小时就可以抽完，但是乙水池的话就需要8×4/5，大于6小时，排除。故本题的正确答案为C选项。

43：单选题、

从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。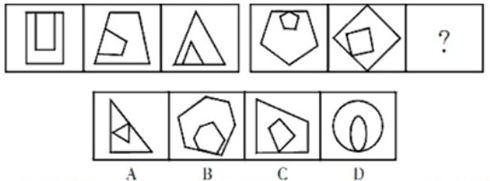

【答案】C

【解析】本题考查位置类旋转问题。两段式题型，在第一段中找到规律：内部图形与外部图形形状相同，并且相交位置（重合边）逆时针旋转，将规律用于第二段中，内部图形与外部图形相交位置（重合点）逆时针旋转。因此，本题答案为C选项。

【拓展】位置类问题是近年来常考的考点。若题干中各个图形组成元素相同，.局部位置发生明显变化，这类题通常考察的是位置类问题。位置类问题通常考察平移、旋转和翻转。区分旋转和翻转的辅助方法是时针法：确定一个起点；确定一个路径；画一个时针。

44：单选题、

从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。

【答案】D

【解析】本题考查数量类直线的个数。两段式题型，在第一段中找到规律：直线个数为14的常数列，将规律用于第二段中，直线个数为12的常数列。因此，本题答案为D选项。

【拓展】数量类问题是近年来常考的考点。若题干中各个图形组成凌乱或者具有明显的数字规律，.通常考察的是数量类问题。数量类问题通常考察点、线、角、面、素的数字规律变化。常见的数字规律有常数列、等差、等比、对称、周期、运算等。线一般分为直线、曲线和一笔画。