几何尺度扩大原理
2022-01-17 09:56:25公务员考试网 文章来源:华图教育
这里主要为大家介绍关于几何尺度扩大理论如何应用以及相对应易错点和难点,还有干扰选项的设置需要大家注意。此类题目并不难,需要大家熟记结论在使用过程中应当注意干扰选项的设置。只要大家理解题干意思和注意选项设置的陷阱,此类问题都能够迎刃而解。
我们来通过一道引题来给大家介绍解题方法。
【引例】如果一个圆柱的底面半径扩大了3倍,那么它的体积扩大了()倍。
A.9
B.8
C.16
D.15
【答案】D
【解析】第一步,本题考查几何问题,属于几何特殊性质类。
第二步,圆柱的底面半径扩大了3倍,那么它的体积扩大了,根据V圆柱=,因为圆柱的底面半径扩大了3倍,则底面半径变为原来的4倍,高不变。所以V现圆柱===16V原圆柱,现在圆柱的面积是原来圆柱的16倍,则扩大了16-1=15倍。
因此,本题选择D选项。
如果把圆柱换成正方形长方形圆形求面积或者周长或者换成正方体长方体圆锥求体积等,如何快速得到正确答案。
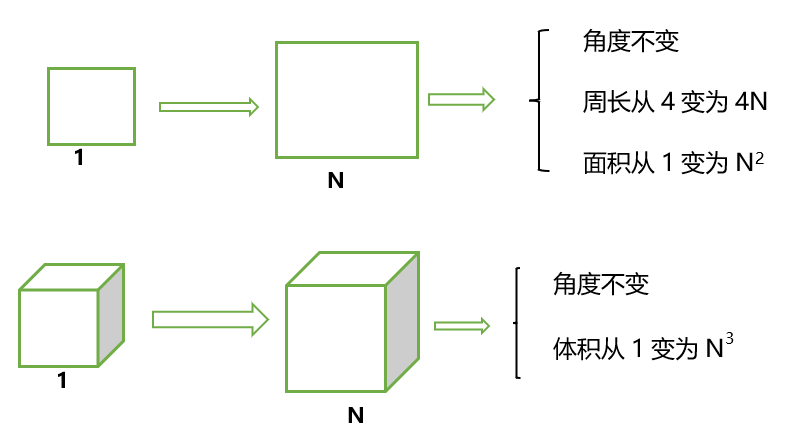
从上述的图片可以得到尺度扩大原理几条结论。当一个图形尺度扩大为原来的N倍,其对应角度保持不变;对应周长变为原来的N倍,则扩大了(N1-1)倍;对应面积变为原来的N2倍,则扩大了(N2-1)倍;体积变为原来的N3倍,则扩大了(N3-1)倍。
我们来再通过两道题再巩固一下上述知识点和做题方法。
1.(单选题)一个圆形的面积是54平方厘米,如果将该圆的半径变为原来的两倍,则该圆的面积变为()平方厘米。
A.81
B.108
C.162
D.216
【答案】D
【解析】第一步,本题考查几何问题,属于几何特殊性质类。
第二步,在圆中,当半径变成原来的2倍时,则面积变为原来的4倍。原来圆形的面积是54平方厘米,则变化后圆的面积应为54×4=216(平方厘米)。
因此,选择D选项。
2.(单选题)某甜品店出售一种规则球形的甜品,该甜品由内部中空的球形面皮(每立方厘米成本0.4元)和实心的芝士球(每立方厘米成本1元)组成。无论甜品大小规格如何,其中的芝士球半径始终为甜品半径的四分之三。已知制作半径为1厘米的该甜品成本约为2.73元,那么要制作半径为2厘米的该甜品,成本约为:
A.5.46元
B.7.45元
C.14.92元
D.21.88元
【答案】D
【解析】第一步,本题考查几何问题。
第二步,由“体积之比等于半径之比的立方”,可得半径为2厘米的该甜品的体积应为半径为1厘米的体积的倍,因此制作半径为2厘米的甜品成本也为半径为1厘米的甜品的8倍。
第三步,成本为元。
因此,本题选择D选项。
通过上述题目可以发现,尺度扩大理论在我们的做题过程中非常重要,可以帮助我们解决很多题目。因此,我们要熟记理论,掌握知识点,更好地运用理论去解题。
【思维导图】
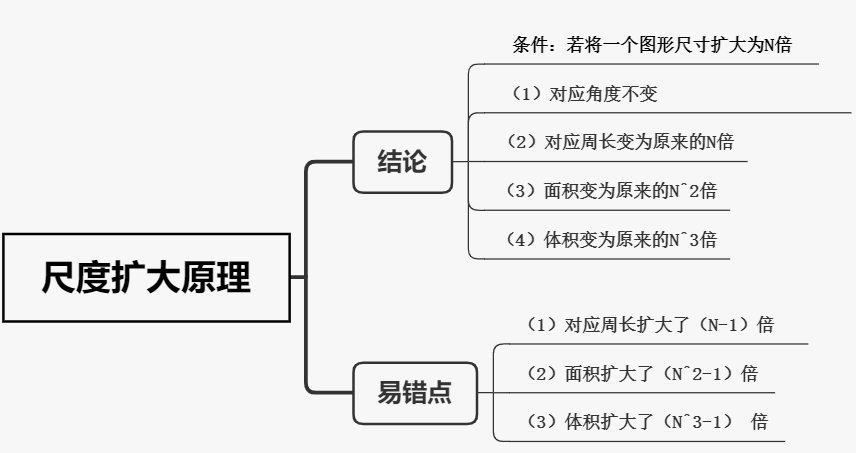
上一篇:插空法解排列组合问题
下一篇:判断推理四大模块备考建议




