其实对于排列组合和概率题目的解题，我们有一些特定的方法技巧可以运用，比如说要求某些元素必须在一起时可以运用捆绑法，要求元素间不相邻时可以运用插空法，将相同元素分组且每组至少拥有一个或多个元素时可以运用隔板法等等。解决排列组合和概率问题可以运用的方法有很多很多，今天我们重点来学习插空法。

1.插空法适用于什么样的题型呢?

插空法是解决排列组合和概率问题常用的方法技巧之一，主要应用于题目中要求某些元素不相邻或不在一起时。简单来说，当遇到排列组合题目中出现不在一起、不相邻这些字眼时，我们就可以考虑该题是否可以运用插空法。

2.怎样运用插空法解题?

运用插空法解决排列组合和概率问题，简单来说可以分为两步：第一步，先将不在一起元素以外的其他元素进行排列(若其他元素之间相同，则排列方式只有一种;若不同，则将这些元素进行全排列);第二步，根据题目条件再将不在一起的元素进行插空(若不在一起元素之间不同，则排列;若相同，则组合)。插空法对于解决元素的不相邻问题非常有用，接下来我们就通过三道真题来学习一下如何运用插空法解题。

【真题1】某学习平台的学习内容由观看视频、阅读文章、收藏分享、论坛交流、考试答题五个部分组成。某学员要先后学完这五个部分，若观看视频和阅读文章不能连续进行，该学员学习顺序的选择有：

A.24种

B.72种

C.96种

D.120种

【答案】B

【解析】第一步，本题考查排列组合问题，用插空法解题。

第二步，观看视频和阅读文章不能连续进行，先把收藏分享、论坛交流和考试答题排列好，共有=6(种)方式，这三部分形成4个空，需在4个空中插入“观看视频”和“阅读文章”，有=12(种)方式，那么共有6×12=72(种)学习顺序。

因此，本题选择B选项。

在这道题中，由于给出的五个元素之间互不相同，因此我们不管是对其他元素还是对不相邻元素都进行了排列。我们先排列了不相邻元素以外的三个元素，其次再将不相邻元素进行插空。接下来我们再来看一道其他元素不同，不相邻元素相同的题目。

【真题2】小区内空着一排相邻的8个车位，现有4辆车随机停进车位，恰好没有连续空位的停车方式共有多少种?

A.48

B.120

C.360

D.1440

【答案】B

【解析】要求4个空车位没有连续的，不相邻问题用插空法，空车位插空排列即可，4辆车停进4个车位，有种方式，4辆车形成5个空，选其中4个空给空车位，有种方式，总共有24×5=120种方式。

因此，本题选择B选项。

在这道题中，其他元素是车，车之间互不相同，因此用排列，不相邻元素是车位，车位和车位之间相同，因此用组合。那会不会有所有元素都相同的不相邻问题呢?接下来我们再来看一道真题。

【真题3】某条道路一侧共有20盏路灯。为了节约用电，计划只打开其中的10盏。但为了不影响行路安全，要求相邻的两盏路灯中至少有一盏是打开的，则共有()种开灯方案。

A.2

B.6

C.11

D.13

【答案】C

【解析】一侧共有20盏灯，打开其中10盏，则熄灭10盏，要求相邻两盏路灯中至少有一盏是打开的，说明熄灭的灯不能相邻，用插空法解题。10盏熄灭的灯插空到10盏打开的灯形成的11个空，共有种。

因此，本题选择C选项。

在这道题中，涉及到的元素是路灯，打开的路灯之间都相同，因此在进行排列时只有一种情况，熄灭的灯之间也相同，在进行插空时进行组合。

通过上述题目可以发现，插空法可以帮助我们很快解决“不在一起或者不相邻”类的排列组合问题，但是在不同的情境中排列和组合的应用也是不同的。因此，我们要多做类似的习题，把相关的知识点掌握透彻，在遇到这类题目时努力做到不丢分。

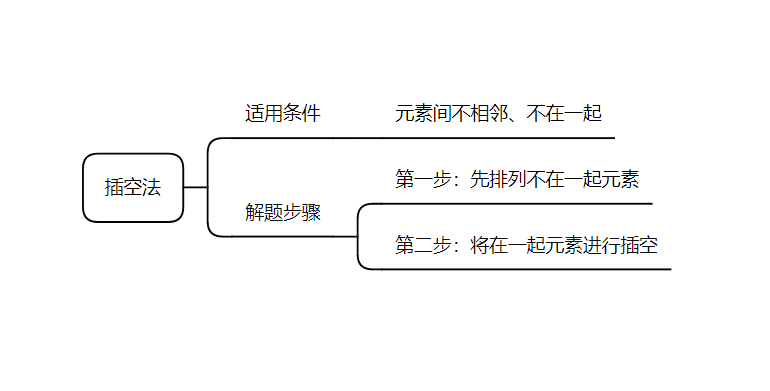
【思维导图】