行测数量关系的知识点大全!!!
2021-06-29 10:57:16公务员考试网 文章来源:华图教育
数量关系知识点
解题方法:数量关系的计算量比较多的如果按部就班的计算是比较消耗时间,所以计算方法就很有必要,能起到事半功倍的效果。
代入排除法:将选项中的答案带入到题干中去,满足所有条件的就是正确的答案。
题型特征
①选项信息充分(选项数据比较多,有两个或者两个以上数据);
②特定题型(不定方程、多位数问题、余数问题、年龄问题、计算复杂类问题等)。
知识点
将选项依次代入题干,符合题意的选项保留,与题干条件有矛盾的选项予以排除。
解题思路
应用代入排除法时要清楚适用的情况,包括选项的特征和具体题型,并掌握最值代入、最简代入、居中代入等技巧。
例题1.某食品厂速冻饺子的包装有大盒和小盒两种规格,先生产了11000只饺子,恰好装满了100个大盒和200个小盒。若3个大盒与5个小盒的饺子数量相等,则每个小盒与每个大盒的饺子数量分别 是( )
A.24只,40只 B.30只,50只 C.36只,60只 D.27只,45只
解:我们根据三个大盒和五个小盒的数量是相等的,100个大盒和200个小盒是11000,再将选项代入,发现只有b选项能够满足题干的要求,其他的都不满足可以快速的选出正确选项b
例题2.一只密码箱的密码是一个三位数,满足三个数字之和为19,十位上的数比个位上的数大2。若将百位上的数与个位上的数对调,得到一个新密码,且新密码数比原密码的数大99,则原密码数是( )
A.397 B.586 C.675 D.964
解:首先三个数字之和为19,将四个选项代入A.B.D都符合。十位上的数比个位上的大二三个选项都符合,接下来考虑第三个条件,百位上的数与个位上的数对调比原来的大99,我们将三个选项带入,只有B符合,选出正确选项B。
代入法在数量关系级的计算中能够起到很大的作用,在题目已知条件的基础上代入答案,不需要经过大量的计算就可以得出答案,值得熟练的掌握。
数字特性法:利用数字的特性比如整除,奇偶,质数等进行快速的筛选答案
题型特征
题目中出现较多分数、百分数、比例、倍数、余数或平均数时,优先考虑倍数特性,对于知和求差、知差求和以及aX+bY=c(不定方程)问题考虑应用奇偶特性。
知识点
倍数特性:
如果a:b=m:n(m、n互质),则a是m的倍数,b是n的倍数;
如果a:b=m:n(m、n互质),则a±b应该是m±n的倍数;
拓展:如果a:b=m:n(m、n互质),则a=b×m/n
解题思路
了解奇偶特性、整除特性、比例倍数特性知识点以及应用题型。当出现某种数字特性匹配的题型或数据特征时要优先考虑该题目能否用数字特性解题。
例题1.方程px+q=99的解为x=1,p,q均为质数,则p*q的值为( )
A.194 B.197 C.135 D.155
解:x=1原式等于p+q=99,p,q和为奇数,所以p,q必定是一奇一偶,而偶数当中是质数的只有2,所以p,q分别书2和97。所以答案是2*97=194选择A选项。
例题2.某企业共有职工100多人,其中,生产人员与非生产人员的人数之比为4:5,而研发人员与非研发人员的人数之比为3:5,已知生产人员不能同时担任研发人员,则该企业不在生产和研发两类岗位上的职工有多少人?
A.20 B.30 C.24 D.26
解:题目中出现了比例而且数字信息不明朗,我们就可以想到用到数字的整除性来解答。首先4:5表示能够被9整除,3:5能够被8整除,也就是说这个数字能被8,9同时整除,同时又是100多的数,只有唯一一个解就是144。那么相应的生产人员是64人,研发人员54人,那么不在生产和研发两类岗位上的职工有144-64-54=26人选择D选项。
数字特性法在题目给出的条件不是很全的时候非常的有用,在解不定方程的时候数字特性法可以根据题目所给的选项快速的解答,同时数字特性放也能够快速的解答,不需要繁琐的列方程就能够得出答案。
赋值法:题目给出的要素之间联系比较紧密的时候,我们可以赋值相关的数特殊值方便我们的计算。
题型特征
1.题目中给出的三个量满足“A=B×C”的比例形式,如果只给定了其中一个量或者未给定任何一个量的时候,采用赋值法。
2.题目未给出明确数值,考虑赋值法。
3.赋值法多应用于工程问题、行程问题、经济利润问题、几何问题和溶液问题等题型。
知识点
赋值法是给予某些未知量一定的特殊值,从而达到便于解决问题的目的,实际上赋值法所体现的是从一般到特殊的转化思想,即把抽象问题具体化,把未知数变成已知数。
解题思路
对于以上题型特征出现,优先考虑赋值法,了解应对题目中哪些数据赋值,以及一些题目赋值公倍数的技巧。
例题1.牧场准备过冬的干草,刚好够100只羊,50头牛,和20匹马过冬,已知一匹马的食量是一只羊的四倍,而一头牛的食量是一匹马和两只羊食量的总和。根据牧场准备的干草总量,如果只养牛的话,可以养( )头
A.60 B.70 C.80 D.90
解:这题中牛,羊,马的食量之间有很明显的数量关系,所以可以运用赋值法来计算。赋值一只羊的食量为1,那么马为4,牛为6,可以得到总得干草量为100+50*6+20*4=480。那么只养牛可以有480/6=80只,正确选项为B。
例题2.某矿业产品公司支付了一批货款,一半用于购进每吨400元的A型石英矿,另一半用于购进每吨600元的B型石英矿,则A,B两种石英矿的平均价格是每吨多少元?
A.480 B.490 C.500 D.510
解:两种石英矿的总价格都是一样的,那我们可以赋值两者都花了600元,那么A型石英矿买了1.5吨,B买了一吨,总体共2.5吨石英砂,共花费1200元,则平均价格为1200/2.5=480所以正确选项为A
赋值法在数量关系当中能够起到很大的作用,在题目中出现了比例出现了相等的关系关联的时候,我们可以考虑能不能用赋值法,尤其是行程与工程问题更加是常常的用得到赋值法,它能很大的程度上帮助我们降低计算量,必须要熟练的掌握。
工程问题和行程问题
工程问题
基本要素:工程总量,工作时间,工作效率
基本公式:工程总量=工作时间*工作效率
题型特征
狭义上通常把修桥、铺路以及明显涉及工程量的问题看成工程问题,但广义上我们通常把完成一件事情需要多长时间的问题看成工程问题。
知识点
核心公式:工作总量=工作时间×工作效率
另:1、当工作效率一定的情况下,工作总量与工作时间呈正比例;
2、当工作时间一定的情况下,工作总量与工作效率呈正比例;
3、当工作总量一定的情况下,工作时间与工作效率呈反比例;
解题思路
1.赋值法
给定时间型:题目中只给定工作时间时,赋工作总量为时间的公倍数;
效率制约型:当题目中不仅给定工作时间,还给出与效率相关的某个逻辑关系时,一般优先寻找效率之间的比例关系进行赋值。
2.方程法
条件综合型:题目中给出了工作量、效率、时间中两个量的已知数据,找出工作量、效率、时间的前后变化,根据题目给出的等量关系列方程或者直接列式求解。
例题1.某单位需要搬家,可以使用甲,乙,丙三个搬家公司。单独完成该搬家任务,甲需要三天,乙需要四天,丙需要十二天;搬家费用分别为甲1000元/天,乙850元/天,丙350元/天。要求在两天内搬完,最少花费多少元?
A.3200 B.3400 C.3550 D.3700
解:题中未出现工作总量但是给出了工作时间,赋值法赋值工作总量为三个数的最小公倍数12,那么效率甲;乙;丙分别是4;3;1,其次我们看谁一天比较划算,甲为250乙为850/3丙为350那么甲更划算让甲做两天还有四的工作量让乙丙各做一天,得出1000*2+850+350=3200所以正确选项为A
例题2.甲,乙,丙三名员工共同修剪6060平方米草地,甲的修剪 效率为30平方米/分钟,乙的修剪效率为40平方米/分钟,丙的修剪 效率为60平方米/分钟。上午,甲7点30分开始修剪,乙7点45分 开始修剪,丙8点15分开始修剪,他们同一时间完成工作,乙用了 ( )分钟
A.56 B.57 C.58 D.59
解:设乙一共用了x分钟,那么甲用了x+15分钟,丙用了x-30分钟,那么根据题意我们可以得到方程30(x+15)+40x+60(x-30)=6060解得x=57所以答案选择B
行程问题
基本要素:路程,时间,速度
题型特征
题目中出现路程、速度、时间等字眼
知识点
基本行程公式:路程 s=速度 v×时间 t。
流水行船问题:顺流航程 S = (V船 + V水) ´ 顺流时间T
逆流航程 S = (V船-V水) ´ 逆流时间T
相遇追及问题: S相 =(V1+V2)T相 S追 =(V1 -V2)T
解题思路
行程问题,是大家熟悉的一类题目,是行测考试的重点。考生一定要掌握行程问题的基础理论,路程、速度、时间的关系要分析清楚,熟练掌握等距离求平均速度、火车过桥及流水行船问题的公式及相遇、追及问题公式,结合方程法、赋值法、比例分析法求解问题
例题1.甲乙两人在相距1200米的直线道路上相向行驶,一条狗与甲同时出发跑向乙,遇到乙之后立即掉头跑向甲,遇到甲后再跑向乙,如此反复,已知甲的速度为40米/分钟,乙为60米/分钟,狗为80米/分钟。不考虑狗调头所耗时间,当甲乙相距100米时狗跑了多少米?
A.1100 B.1000 C.960 D.880
解:根据题意甲乙一共行走了1100米,两者是相向而行所以两者的走1100米的速度可以看做为100米/分钟,那么两者相距1200米到相距100米花费的时间为11分钟,那么狗也走了11分钟,那么狗走的距离为11*80=880,真确选项为880
例题2.甲乙丙分别骑摩托车,乘大巴,打的从A地去B地。加的出发时间分别比乙,丙早15分钟,20分钟,到达时间比乙,丙都晚5分钟。已知甲乙的速度之比为2:3,丙的速度为60 千米/小时,则AB两地的距离是( )
A.75千米 B.60千米 C.48千米 D.35千米
解:根据题意可得甲比乙多用时20分钟,比丙多用时25分钟,甲与乙的速度之比为2:3那么在路程相同的情况下时间之比为反比3:2,也就是甲比乙多一份时间为20分钟,那么甲总用时60分钟,就可以推出丙用时35分钟,那么AB两地距离为35千米,正确选项为D
在工程问题和行程问题当中,两者的基本公式非常的相似都是三个元素有乘除的等式关系,当他们当中的一个元素定下来的时候,另外两个元素一定会呈现相信的正反比,可以根据这个来解题。在工程问题方面解题思路是多样的有方程法有赋值法,行程方面的计算要注意的就是单位的换算。两者在考试中是每年都会出现的常客,所以必须有把握把这种题做会。
经济利润问题
基本要素:成本,利润,利润率,折扣,售价,原价
题型特征
题目中出现售价、成本、利润、折扣等字眼。
知识点
核心公式:
1.利润=单价-成本;期望利润=定价-成本;实际利润=售价-成本;
2.利润率=利润÷成本=(售价-成本)÷成本=售价÷成本-1;
3.售价=定价×打折(“二折”即售价为定价的20%);
4.总售价=单价×销售量;总利润=单件利润×销售量
经济利润类的题目考的几率很大,这种题计算量多但是不是特别的难,很容易就做出来了。这类题的主要做法就是方程法和赋值法,经济利润类额题目主要分为三大类分别是基础公式类,分段计时类,统筹类,虽然类别不同本质的区别都是运用公式,所以要熟练并灵活的运用公式。
排列组合与概率
计数方法:分步分类和排列组合
排列与组合的区别:前者与顺序有关,后者与顺序无关。
加法原理和乘法原理
加法原理:若完成一件事,可以根据某个条件分为几种情况,各种情况都能独立完成任务,则将多种情况计算出的结果相加,所得的和为完成这件事的种类数。
乘法原理:若完成一件事,需要划分成多个步骤依次完成,每个步骤内的任务之间没有交叉,则将每个步骤计算出的结果相乘,所得的积为完成这件事的种类数。
基本公式
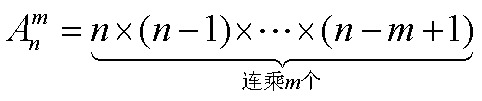
排列公式:
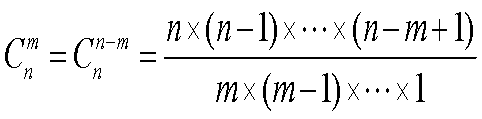

组合公式:
例题1.将五个不同颜色的锦囊放入4个不同的锦盒里,如果允许锦盒时空的,则所有可能的放置方法有( )
C45 B.45种 C.54种 D.A45种
解:因为不考虑锦盒的状态,所以本题每个锦囊都有四个锦盒可 以选择都是四种可能,而五个锦囊是分步操作的所以是4*4*4*4*4也就是45种,正确选项选择B
例题2.某公司现有6箱不同的水果,安排三个配送员送到A,B,C三个不同的仓库,其中A地1箱,B地2箱,C地3箱,问配送方式有( )
A.60种 B.180种 C.360种 D.420种
解:分步来看,首先A地安排水果有6种,接下来考虑B仓库的情况,在剩下的5箱水果中选取两箱不考虑顺序为![]() ,那么剩下的箱子全部去C地,在考虑配送员与配送地的问题,是有顺序的排列为
,那么剩下的箱子全部去C地,在考虑配送员与配送地的问题,是有顺序的排列为![]() ,那么最终为6*10*1*6=360种,正确选项为C。
,那么最终为6*10*1*6=360种,正确选项为C。
在排列组合的问题当中,分步,分类,排列组合的公式是最本的要素,以后的所有问题都是离不开的,要熟知排列和组合的区别并对两者的计算公式都要有明显的区分。
方法与技巧
基本的方法技巧:插空法,捆绑法,错位排列
①捆绑法:如果题目要求一部分元素必须在一起,需要先将要求在一起的部分视为一个整体,再与其他元素一起进行排列。
②插空法:如果题目要求一部分元素不能在一起,则需要先排列其他主体,然后把不能在一起的元素插空到已经排列好的元素中间。
③错位排列:有n个元素和n个位置,如果要求每个元素的位置与元素本身的序号都不同,则n个元素对应的排列情况分别为, 0种,1 种, 种,2 种,9 种,44种。
例题1.单位组织拔河比赛,每支参赛队伍由3名男职工和3名女职工组成,假设比赛时要求3名男职工不能全连在一起,则每支队伍有多少种不同站位方式( )
A.432 B.504 C.576 D.720
解.题目要求的是求不能全部连在一起的方式,我们可以侧面思考,求出全部连在一起的数量,再拿总数减去就可得到所求的数。首先总数为![]() ,三个全待一起分步进行,先排列男职工有
,三个全待一起分步进行,先排列男职工有![]() ,再排列女职工有
,再排列女职工有![]() 种,将男职工捆绑在一起插空到女职工的空隙里面有4种可能,那么全部在一起有6*6*4=144,那么不全连在一起的数量有720-144=576,正确选项、为C选项。
种,将男职工捆绑在一起插空到女职工的空隙里面有4种可能,那么全部在一起有6*6*4=144,那么不全连在一起的数量有720-144=576,正确选项、为C选项。
例题2.某城市一条道路上有四个十字路口,每个十字路口至少有一名交通协管员,现将8个协管员名额分配到这4个路口,则每个路口协管员名额的分配方案有:
A.35种 B.70种 C.96种 D.114种
解.本题比较特殊,首先根据隔板法的使用条件,将n个相同的元素分给m个组,每组至少得一个,总的分配方法为![]() ,很显然此题适用隔板法,直接套入公式为
,很显然此题适用隔板法,直接套入公式为![]() ,真确选项为A。
,真确选项为A。
在排列组合的计算当中,方法与技巧是非常重要的有些时候直接计算,计算量非常的大甚至非常的困难无从下手,我们可以通过各种方法来简化计算量,侧面计算增加解题的方法,有些技巧例如隔板法也是一种简便的工具符合要求的直接代入公式就可以,所以在做题中需要灵活的运用计算方法与技巧,背熟相关的公式。
概率问题
基本概率:某种情况发生的概率=满足条件的情况数÷总的情 数。
分类概率:某项任务可以在多种情况下完成,则分别求解满足条件的每种情形的概率,然后将所有概率值相加。
分步概率:某项任务必须按照多个步骤完成,则分别求解特定条件下每个步骤的概率,然后将所有概率值相乘。
逆向公式:正面的概率=1-反面的概率
例题1.小李从标有1,2,3,4,5的五张卡片中,任取两张卡片,则两
张卡片上的数字相差2的概率是多少?
A.1/5 B.2/5 C.3/4 D.3/10
解.概率=满足条件的情况数/总的情况数,从五张卡片中任取两张,总的情况数![]() ;满足两张卡片上的数字相差 2 的情况数分别为:1、3;2、4;3、5 共 3 种,概率为 3/10 因此,选择 D 选项。
;满足两张卡片上的数字相差 2 的情况数分别为:1、3;2、4;3、5 共 3 种,概率为 3/10 因此,选择 D 选项。
例题2.某单位的一个科室从10名职工中随机挑选2人去听报告,要求女职工人数不得少于1人。已知该科室女职工比男职工多2人,小张和小刘都是该科室的女性职工,则她们同时被选上的概率在以下哪个范围内?
A.3%到5%之间 B.小于2% C.2%到3%之间 D.大于5%
解.由“10名职工”、“女职工比男职工多2人”可知该科室女职工为6人、男职 工为4人。总情况数包含两类:①女职工1人、男职工1人,有![]() (种);②女职 工2人,有
(种);②女职 工2人,有![]() (种);共24+15=39(种)。概率=满足的情况数÷总情况数,满足的情况数只有1种即小张和小刘同时被选上,则所求概率为1÷39≈2.61。 因此,选择 C 选项。
(种);共24+15=39(种)。概率=满足的情况数÷总情况数,满足的情况数只有1种即小张和小刘同时被选上,则所求概率为1÷39≈2.61。 因此,选择 C 选项。
例题3.某公司对10个创新项目进行评选,选出最优秀的3个项目投入运行。小张随机预测3个项目将会入选。问他至少猜对1个入选项目的概率在以下哪个范围内?
不到50% B. 50%~60% C. 60%~70% D. 超过70%
解.本题问至少猜对 1 个入选项目的概率为多少,正面求解较为困难,从反面求解,至少猜对 1 个的概率=1-全猜错的概率。总的情况数为从 10 个中任意挑选三个,情况数为![]() ,全猜错的情况为从错误的七个里面任意挑选三个,情况数为
,全猜错的情况为从错误的七个里面任意挑选三个,情况数为![]() ,全猜错的概率为P=7/24,因此至少猜对一个的概率为1-7/24=17/24,约等于70.8%,选择D选项。
,全猜错的概率为P=7/24,因此至少猜对一个的概率为1-7/24=17/24,约等于70.8%,选择D选项。
概率的计算往往是与排列组合和乘法原理和加法原理相关的,很多的计算都是需要用到之前学习的一些公式和思路。当我们计算概率是永远要记住概率的最大值是1最小值为0。而且概率的计算必须得要不遗漏不多算。
.




