2019-11-29 10:56:59 社区工作者考试 http://www.huatu.com/shehui/ 文章来源:华图教育
【导读】华图社区工作者考试频道同步华图教育发布:社区工作者考试备考:典型性容斥问题举例,华图教育为大家整理了行测备考相关知识供广大考生复习,更多备考技巧请持续关注华图教育,详细信息请阅读下文!
在历次考试中,容斥问题基本上隔三年就会出来一次,这类问题比较简单,算是给考生送分的题目,希望各位考生能够把握这种题型。下面我们从一道国考题来剖析下两集合容斥的解题技巧。
【例】工厂组织职工参加周末公益活动,有80%的职工报名参加,报名参加周六活动的人数与报名参加周日活动的人数比为2:1,两天的活动都报名参加的人数为只报名参加周日活动的人数的50%。问未报名参加活动的人数是只报名参加周六活动的人数的:
A. 20% B. 30%
C. 40% D. 50%
思路分析:
1、根据题干,可判定这个题为两集合容斥问题。
2、又发现题干中有人数比为2:1,要大胆采用赋值法。本题是一道将赋值法和两集合容斥结合在一起的题型,具有典型性。
解题步骤:
第一步,标记量化关系“比”、“都”、“只”、“未”、“只”。
第二步,如图所示,根据“都”报名为“只”报名周日人数的50%,赋值都报名的人数为1,可得“只”报名周日的人数为2,报名周日的人数为1+2=3;由人数“比”为2:1,可得报名周六的人数为3×2=6,“只”报名周六的人数为6-1=5,故总的报名人数为5+1+2=8。
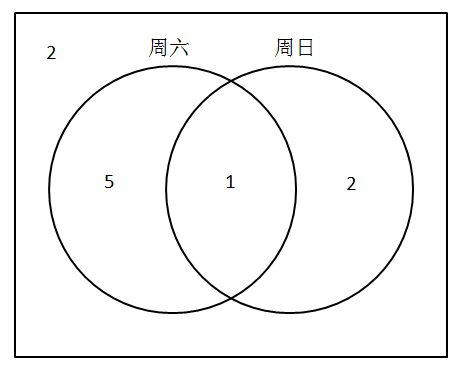
第三步,由总人数为8/80%=10,可知“未”报名人数为10-8=2,故“未”报名人数是“只”报名周六的2/5=40%。因此,选择C选项。

贴心微信客服

Q群福利小灶