2022年省考行测资料单类解题之《牛吃草怎么解》

• 资料分析题型
• 资料分析公式
• 数资易错点
• 数量关系公式
• 常识百年党史
• 全年时政热点

*资料包涵盖但不限于以上内容

扫码领福利

保存小程序码至
手机进行扫码

在申论和行测两门考试中，行测的数量关系模块一向是同学们的痛楚，在这个模块大家经常会“剃光头”，难办得很，那么有没有什么小技巧能够帮助我们解决这样的问题呢?这里还真就有这样一类题型，一旦出现，那么就是白送分的题目，那就是牛吃草问题。接下来我们一起学习牛吃草问题到底如何解决。

学习一个题型之前我们一定要先学会辨认题型，如果我连题型都无法辨认出来，那么在考试当中即便我真的记住了解题套路，也会因为无法认出这个题型而错过，从而失去拿分机会。那么牛吃草问题有什么样的特征呢?

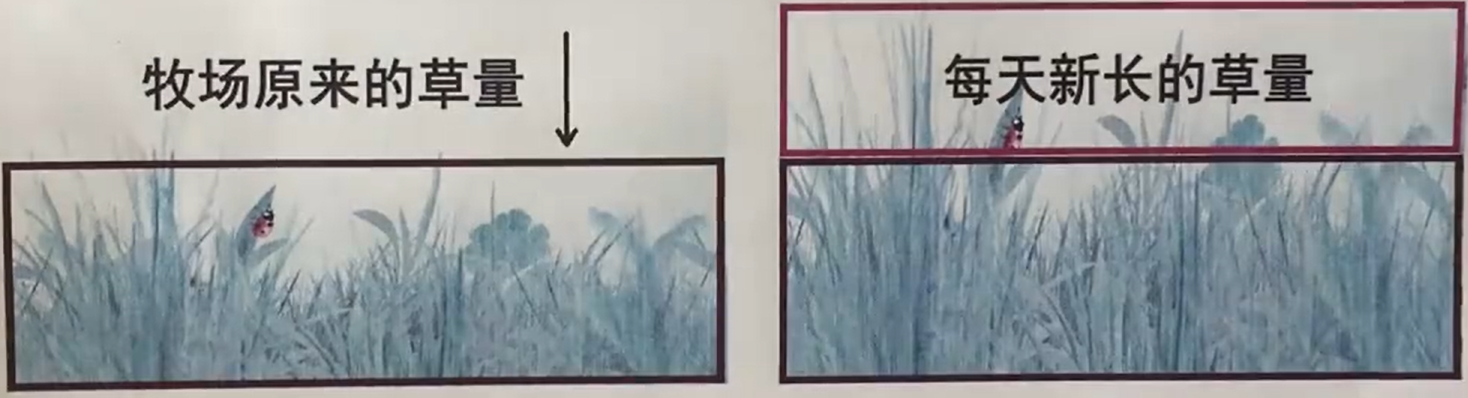
大家试想牛吃草与我们人吃饭有什么区别呢?如果你不往碗里添饭，那么吃一会儿饭就会吃完，但是牛吃草的过程中，草一边在被吃，但是一边又在生长，因此牛吃草的题型的特点就是有涨有耗。类似的模型还有窗口售票、泳池给排水等。

那么这类题该如何求解?只需要一个公式：

(其中：y为原有量;n为消耗速度;x为增长速度;t为时间。)

即可解决。以上公式中，y的原有量一般指开始消耗前，草的数量有多少，原始的草量越多，原有量越大;n的消耗速度一般指牛的数量，牛的数量越多，消耗速度越大;x的增长速度一般指草生长的速度;t的时间一般指以“n-x”的速度消耗完所有原有量y所花费的时间。我们只需要将具体题目当中的对应模型的量代入到公式当中就可以了。那么接下来让我们尝试做两道题目。

【例1】火车站售票窗口一开始有若干乘客排队购票，且之后每分钟增加排队购票的乘客人数相同。从开始办理购票手续到没有乘客排队，若开放3个窗口，需耗时90分钟，若开放5个窗口，则需耗时45分钟。问如果开放6个窗口，需耗时多少分钟?

A、36

B、38

C、40

D、42

【答案】A

【解析】本题考查牛吃草问题;

第一步，题目中的窗口排队模型可以转换为牛吃草模型，队伍原有长度(人数)为原有量y;窗口开放越多，队伍长度(人数)减少越快，即窗口在“消耗”队伍的长度，因此窗口数量对应消耗速度n;每分钟增加排队购票的乘客人数使得队伍长度(人数)增长，因此对应增长速度x，从开始办理购票手续到没有乘客排队所耗时间对应为时间t，由“若开放3个窗口，需耗时90分钟，若开放5个窗口，则需耗时45分钟”代入到公式中可以得到方程组：

解得：

所以原公式转换为。现在想要开放6个窗口，即令n=6，代入到公式中可以得到，解得t=36。

因此，选择A选项。

【例2】某河段中的沉积河沙可供80人连续开采6个月或60人连续开采10个月。如果要保证该河段河沙不被开采枯竭，问最多可供多少人进行连续不间断的开采?(假定该河段河沙沉积的速度相对稳定)

A、25

B、30

C、35

D、40

【答案】B

【解析】本题考查牛吃草问题;

第一步，题目中的河沙开采可以转换为牛吃草模型，河道原有沉积泥沙为原有量y;开采的人数越多，开采速度越快，消耗原有泥沙的速度越快，因此开采的人数对应消耗速度n;河沙沉积速度稳定，河沙沉积速度即对应河沙的增长速度x;开采完所有河沙的时间对应时间t，由“某河段中的沉积河沙可供80人连续开采6个月或60人连续开采10个月”带入到公式中可以得到方程组

解得：

即原有沉积的河沙对应300人一个月的开采量，每月沉积河沙对应30人一个月的开采量，若要进行不间断的开采，则每个月开采的速度不可以超过河沙沉积的速度，因此最多可以供30个人进行连续不间断的开采。

因此，选择B选项。

通过以上两题，大家也可以看出，只要我们在考试当中能够辨认出一道牛吃草问题，那么拿下这一分也将不成问题。

相关内容推荐：