2022省考行测备考干货之数量关系方阵问题知多少

在数量关系中有着一些较为简单和独立的小题型，这种小题型通常以难度低、考查频率低为特点。考生在备考过程中应该以不放过任何一个可能的得分点为目标，学习掌握该类题型的题目特征和解题方法，这样才能最大限度地实现自己的上岸梦想。

所以今天，我们来认识一种小题型：方阵问题。

方阵问题是什么

题目中出现“方阵”字眼、人数排列成正方形等等描述，并且求解的对象也是跟人数相关的题目，我们就称之为方阵问题。

例如图中所示，就为一个五阶方阵，即边长是5的方阵。

方阵问题的技巧和公式

1、方阵的总人数

由上图可知，方阵就是一个点构成的正方形，那么总人数应该等价于正方形的面积。所以N阶方阵的总人数为边长人数的平方。

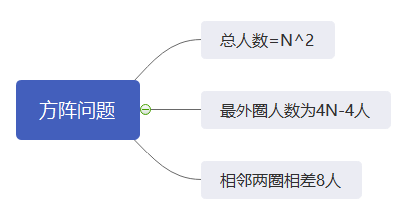
即公式：总人数=N^2

2、方阵的最外圈人数

我们很容易想到最外圈的人数应该是边长的四倍，但是这样去计算的话，站在四个角的人就被我们重复计算了。所以还应该减去站在四个角被重复计算一次的四个人，所以最外圈人数为边长的四倍再减四。

即公式：最外圈为4N-4人

相邻两圈相差人数

根据上述公式可得最外圈的边长为N，则总人数为4N-4人，次外圈边长为N-2人，所以总人数为4(N-2)-4即为4N-12人。那么最外圈和次外圈的差值为：4N-4-(4N-12)=8人。所以相邻两圈相差人数为8人。

实战运用

【例1】参加某运动会的全体运动员在开幕式上恰好排成一个正方形，有两行两列的运动员离场后，运动员人数减少64人，则参加该运动会的运动员人数为：

A.225B.256C.289D.324

解析：我们看到全体运动员恰好排成了一个正方形，所以应该是一个方阵。两行两列运动员离场后，那么根据图形观察，设原本一行的人为X人。那么离开的人数中，两行即为2X，但是此时每一列都走了2人，所以两列的人数应该是2X-4。即总共离场的人数为4X-4=64。可以解得X=17。所以总人数为17×17=289人。选择C选项。

【例2】某学校要将全体运动员排成方阵，老师按人数粗略估计进行第一次排列，发现多出99人，于是又将每行和每列多加了4人进行排列，发现缺少37人。问学校共有运动员多少人?

A.256B.289C.324D.361

解析：我们设第一次排列的每行每列的人数为X人。所以可以根据总人数不变构建等式。方阵总人数为X*X+99=(X+4)(X+4)-37，解得X=15人。

所以总人数应该是15×15+99=324人。选择C选项。

【省考面试礼包】|【省考面试系统提升】|【省考面试图书】|【面试题库】

相关内容推荐：