2022省考行测行程问题中的等距离平均速度

• 资料分析题型
• 资料分析公式
• 数资易错点
• 数量关系公式
• 常识百年党史
• 全年时政热点

*资料包涵盖但不限于以上内容

扫码领福利

保存小程序码至
手机进行扫码

行程问题几乎是每次行政职业能力测试数量关系模块的必考题型，也是众多考生复习时觉得比较有难度的一类问题。今天我给大家介绍一下基本行程问题中的等距离平均速度题型。

所谓等距离平均速度，通常指一个物体分别以两个不同大小的速度，通过一段相等的路程的平均速度。他的基础运动模型如下：

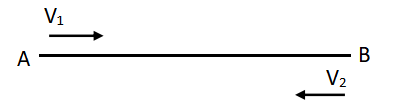
需要注意的是，这里所说的等距离是指以速度V1走过的路程与以速度V2走过的路程相等。在具体应用这个公式时一定要判别清楚题目是否出现这种路程相等的情形。

具体的考题中，简单的题目运动模式会与上面的基本模型比较相近，比如：

【例1】某人开车从A镇前往B镇，在前一半路程中，以每小时60公里的速度前进;而在后一半的路程中，以每小时120公里的速度前进。则此人从A镇到达B镇的平均速度是每小时多少公里?

A.60B.80

C.90D.100

在本题中，前一半路程速度为每小时60公里，后一半路程速度为每小时120公里。如下图，前一半路程长度与后一半路程长度相等，即AC=CB。

近年来的一些新题目，在考查等距离平均速度公式时，设计的运动轨迹与基础模型还是有一些差异的，这类题目的难度要比【例1】这样的基础题目大一些，比如：

【例2】小明每天从家中出发骑自行车经过一段平路，再经过一道斜坡后到达学校上课。某天早上，小明从家中骑车出发，一到校门口就发现忘带课本，马上返回，从离家到赶回家中共用了1个小时，假设小明当天平路骑行速度为9千米/小时，上坡速度为6千米/小时，下坡速度为18千米/小时，那么小明的家距离学校多远?

A.3.5千米B.4.5千米

C.5.5千米D.6.5千米

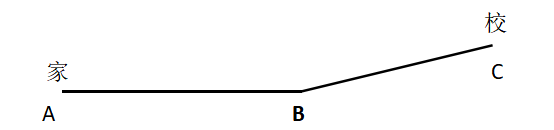
本题中，小明家到学校的路线如上图所示，根据题意，题目中出现了三个速度数据，能够满足应用等距离平均速度公式的是坡路部分，即BC段，而不是从A到C与从C到A。所以，求解时，我们可以先计算BC段的平均速度，再结合AB段的速度确定从家到学校的距离。

相信，通过将以上两个题目与基本运动模型进行对比讲解后，大家能够对等距离平均速度公式的使用方法理解的更深入。

相关内容推荐：