2022-01-04 13:29:36 公务员考试网 
 文章来源:云南分院
文章来源:云南分院
各位正在备考的小伙伴,今天我们一起来学习余数特性在数量关系量解方程中的应用。方程法是数量关系解题方法的第一方法,能帮助我们解决很多题目,但方程法也有其弊端,解方程需要花费的时间较多,今天我们就一起来学习一个分析方程的技巧-余数特性,来帮助我们更好的去分析方程。
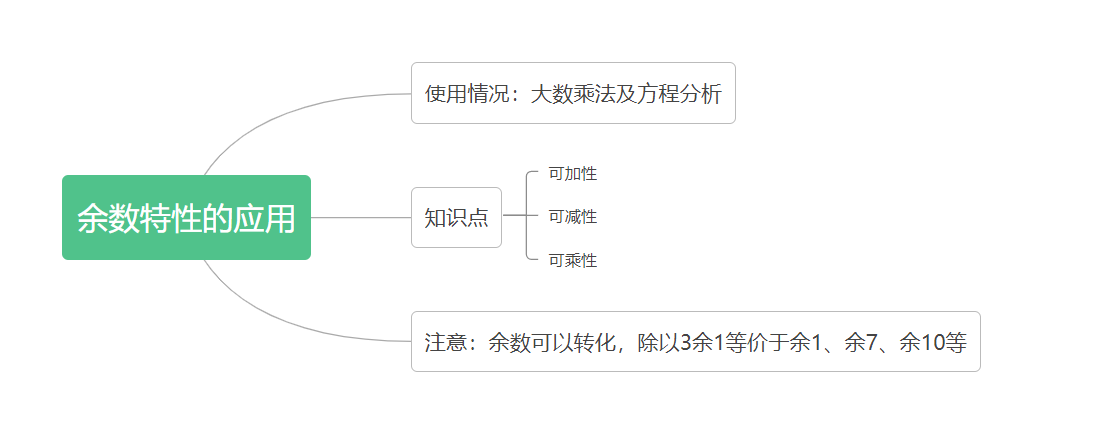
首先我们来看知识点:余数具有可加性、可减性、可乘性(常用除以3、9等数据)。
可加性:28+16=44,44除以3余2,可以拆分为28除以3余1,16除以3余1,余1+余1=余2;
可减性:28-16=12,12除以3余0,可以拆分为28除以3余1,16除以3余1,余1-余1=余0;
可乘性:28×16=448,448除以3余1,可以拆分为28除以3余1,16除以3余1,余1×余1=余1;
注:余数是可以转化的,比如25除以3,商为8余1,商为7余4,商为6余7,即除以3余1、余4、余7是等价的
接下来我们通过几个例题来看一下余数特性的具体应用:
【例1】35246×17693=()
A.623637478 B.623627478 C.623617478 D.623607478
解析:35246除以9余2,17693除以9余8,余2×余8=余16,除以9余16等价于除以9余7,因此答案选项除以9必余7。A选项除以9余1,排除,B选项除以9余0,排除,C选项除以9余8,排除,D选项除以9余7,正确,因此选择D选项。
【例2】某足球比赛售出40元、80元、120元门票共2000张,其中80元的门票数是120元的门票数的2倍,比赛门票收入共12万元。则40元门票售出多少张?
A.1000
B.1150
C.1200
D.1250
解析:本题考查基础应用题,设40元的门票有x张,120元的门票有y张,则80元的门票有2y张,根据总数为2000张可以列出等式,x+3y=2000,3y除以3余0,2000除以3余2,根据余数的可加性可分析出x除以3余2,即余2+余0=余2,A除以3余1,排除;B除以3余1,排除;C除以3余0排除;D除以3余2,正确,因此选择D选项。
【例3】某次田径运动会中,选手参加各单项比赛计入所在团体总分的规则为:一等奖得9分,二等奖得5分,三等奖得2分。甲队共有10位选手参赛,均获奖。现知甲队最后总分为61分,问该队最多有几位选手获得一等奖?
A.3
B.4
C.5
D.6
解析:本题考查不定方程问题,设获得一等奖的有x位选手、获得二等奖的有y位选手、获得三等奖的有z位选手。根据共10位选手参赛和总分为61分,可列不定方程组:x+y+z=10①,9x+5y+2z=61②,②-①×2可得:7x-3y=41。通过余数特性分析,41除以3余2,3y除以3余0,则7x除以3余2,又因为7除以3余1,因此x除以3余2,只有C选项满足,选择C选项。
最后将今天知识点给大家整理为思维导图:

相关内容推荐:

贴心考公客服

贴心专属客服

报名条件?
岗位选择?
笔试科目?
面试方式?
......

 在线客服×
在线客服×