2022-01-04 13:09:22 公务员考试网 
 文章来源:湖南分院
文章来源:湖南分院
湖南省考行测数量关系中的排列组合是每年必考的题型,排列组合中有几个特殊模型,包括捆绑、插空、隔板、错位排列、环形排列等,今天小编先给大家介绍一下捆绑和插空。
关于捆绑和插空应用的题型及做法见下表:
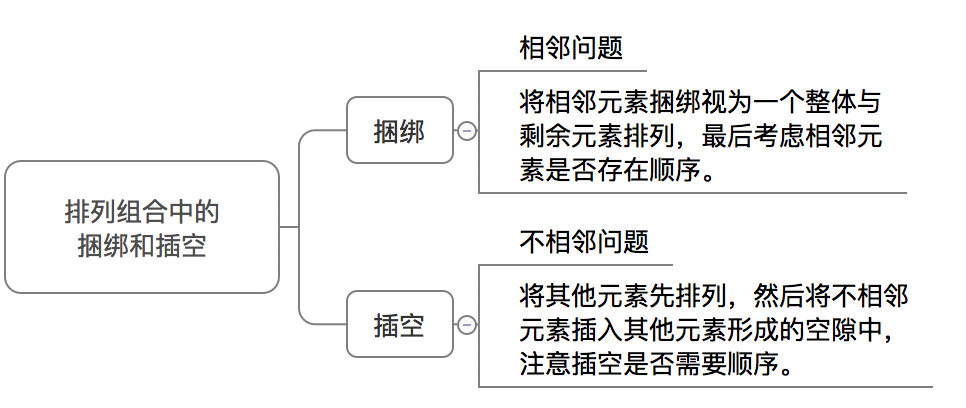
| 类型 | 应用题型 | 做法 |
| 捆绑 | 相邻问题 | 将相邻元素捆绑视为一个整体与剩余元素排列,最后考虑相邻元素是否存在顺序。 |
| 插空 | 不相邻问题 | 将其他元素先排列,然后将不相邻元素插入其他元素形成的空隙中,注意插空是否需要顺序。 |
引例1:A、B、C、D、E五人站成一排,其中A、B两人必须站一起,求有多少种站法?
分析:A、B两人必须站一起,说明A、B两人要相邻,相邻的问题用捆绑法。
第一步,我们先将A、B两人捆绑在一起看成一个人,然后与C、D、E三个人进行全排列情况数为;
第二步,考虑A、B两人内部的全排列顺序情况数为;
第三步,总站法有×=24×2=48。
接下来我们来看一道真题。
【例1】某场科技论坛有5G、人工智能、区块链、大数据和云计算5个主题,每个主题有2位发言嘉宾。如果要求每个主题的嘉宾发言次序必须相邻,问共有多少种不同的发言次序?
A.120
B.240
C.1200
D.3840
分析:要求每个主题2位嘉宾发言次序必须相邻,相邻问题用捆绑。
第一步,分别将5个主题的每2位嘉宾捆绑在一起看成一个人,先给5个捆绑进行排序情况数为=120;
第二步,5个捆绑内每2个人都有=2的内部全排列顺序;
第三步,最终的发言情况数为×()5=120×32>120×30=3600。
因此,选择D选项。
大家学会用捆绑法解决相邻问题了吗?下面我们来看不相邻问题。
引例2:A、B、C、D、E五人站成一排,其中A、B两人不能站一起,求有多少种站法?
分析:A、B两人不能站一起,即A、B不相邻,不相邻的问题用插空。
第一步,先排C、D、E三人,情况数为;
第二步,C、D、E三人产生4个空,从4个空选出2个空将A、B分别放进去,情况数为(A、B两人不同,插空时有顺序);
第三步,总情况数为×=6×12=72。
下面我们来看一道真题。
【例2】因电路改造,电力公司计划未来十天对某小区选择三天停电,要求不能连续两天停电,则共有多少种停电方案?
A.35
B.56
C.84
D.120
分析:题目要求不能连续两天停电,即要求停电不相邻,不相邻的问题用插空。
第一步,不停电的7天产生8个空;
第二步,从8个空选3个空,有情况数=56(停电的3天相同,不考虑顺序)。
因此,选择B选项。
关于捆绑和插空大家学会了吗,赶紧找些题目练习起来吧。

相关内容推荐:

贴心考公客服

贴心专属客服

报名条件?
岗位选择?
笔试科目?
面试方式?
......

 在线客服×
在线客服×