2022年省考行测预测之立体一笔画

• 资料分析题型
• 资料分析公式
• 数资易错点
• 数量关系公式
• 常识百年党史
• 全年时政热点

*资料包涵盖但不限于以上内容

扫码领福利

保存小程序码至
手机进行扫码

近年，行测判断推理模块创新考题频出，令许多考生措手不及，黯然神伤。尤其是图形推理规律类部分，更是将“平面考点立体化”的理念不断地推陈出新，创意十足。如下题：

【例】从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性：

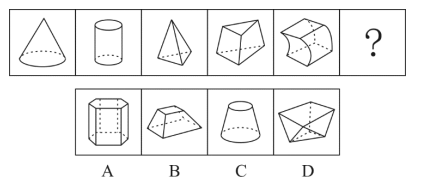
题干及选项所有图形均为立体图，很多考生误以为必定考查立体类考点，其实不然，此题考点却是立体图形中面的个数，分别为2、3、4、5、6，故问号处立体图形面的个数为7，D选项为正确答案。以往“面”的考查主要体现在平面几何图形中，而此题却将平面图形考点由此及彼，运用在了立体图中，十分有趣。“平面考点立体化”的理念在这道题中清晰地体现。预测以后会有更多“平面考点立体化”的考题出现，而可能性最大的估计得是“立体一笔画”。

常规的平面一笔画作为国联考的常考题型，大部分备考考生对其并不陌生，且华图教育也总结了快速判断一笔画的两个必备条件——①图形为整体;②图形奇点数为0或2。如果将一笔画考点运用在立体图中，上述判断技巧是否依然成立呢?答案是肯定的!依然适用。无论是平面图还是立体图，构建一笔画的方式只有两种：一、起笔点和落笔点不重复，故存在两个奇点，这叫“有始有终”;二、起笔点和落笔点重复，故不存在奇点，这叫“始终如一”。

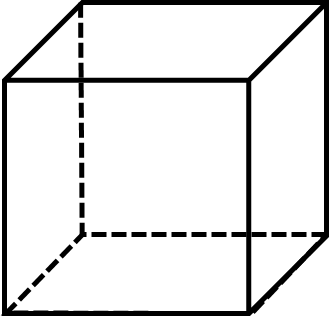
例如，上图为正六面体，共有十二条棱线，那么是否能够一次性不重复的走完所有棱线呢?正六面体为整体，接下来直接判断奇点数是否满足0或2即可。由于正六面体共有8个顶点，且每一个顶点都发散出了3条棱，故正六面体的奇点数为8，不满足上述必要条件，不能一笔画成。

【预测题】下面哪一个立体图形能一次不重复地经过所有棱：

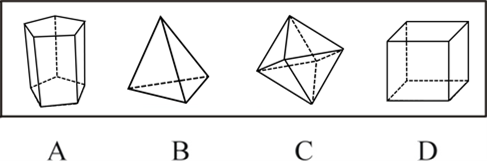
【解析】题目设问为“哪一个立体图形能一次不重复地经过所有棱”，故此题考查“立体一笔画”，利用一笔画两个必备条件进行判断：①图形为整体;②图形奇点数为0或2。由于所有立体图均为整体，故接下来细致判断各图形奇点数即可。A项为五棱柱，所有顶点发散棱线数都为3，均为奇点，该图形共有10个奇点，不能一次不重复地经过所有棱，排除;B项为三棱锥，所有顶点发散棱线数都为3，均为奇点，该图形共有4个奇点，不能一次不重复地经过所有棱，排除;C项为八面体，所有顶点发散棱线数都为4，都不是奇点，该图形共有0个奇点，能一次不重复地经过所有棱，当选;D项为正六面体，所有顶点发散棱线数都为3，均为奇点，该图形共有8个奇点，不能一次不重复地经过所有棱，排除。故该预测题答案为选项C。

相关内容推荐：