2022省考行程问题中匀加速运动的处理方法

• 资料分析题型
• 资料分析公式
• 数资易错点
• 数量关系公式
• 常识百年党史
• 全年时政热点

*资料包涵盖但不限于以上内容

扫码领福利

保存小程序码至
手机进行扫码

行程问题几乎是行测中数量关系模块的必考题型，通常分为基本行程问题和相遇追及问题，在基本行程问题中有一类比较特殊的问题:匀加速运动。匀加速运动每隔几年就会考查一次。今天我就给大家介绍一下匀加速运动题目的求解方法。

所谓匀加速运动，是指运动物体的速度会随着时间均匀增加。速度与时间的关系如下图：

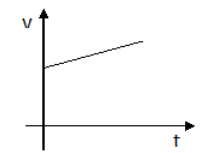
速度公式可以表示成，v=v1+at，其中v1表示物体运动的初始速度，a表示加速度，v表示在时间t时刻物体的运动速度。

在匀加速运动中如果需要求解物体的运动路程，我们可以借助上面的图形，更直观的理解如何计算。比如：

【例1】(2020年北京)一辆汽车在高速公路上以60公里/小时的速度匀速行驶，此时司机开始以固定的加速度进行加速，加速后50秒内，汽车行驶了1公里。则汽车从开始加速，到加速至高速公路的速度上限120公里/小时需要多长时间?

A.100秒B.125秒

C.150秒D.180秒

在本题中，初始速度v1=60公里/小时，设50秒后速度为v

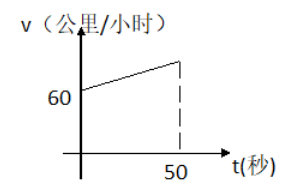
将初始速度看作梯形上底的长度，50秒对应的速度看作梯形下底的长度，50秒看作梯形的高，图中梯形的面积即是速度与时间的乘积，即50秒内汽车走过的路程。根据题意“加速后50秒内，汽车行驶了1公里”，这个梯形的面积为1。50秒=小时，代入s的表达式，有s=×(60+v)t，得1=×(60+v)×，解得v=84公里/小时，相当于每50秒速度增加24公里/小时，从60增加到120，需要增加60公里/小时，需要时间为50秒×=125秒，因此选择B选项。

题目如果给出加速度，此时求解匀加速运动的路程，可以用S=v1t+at²来求解，其中v1表示初始速度，t表示运动时间，a表示加速度。

【例2】(2020年0725四川)甲、乙两辆小车从相距100米的轨道两端同时出发相向而行，甲车以2米/秒的速度匀速行驶，乙车从静止状态开始以1米/秒²的加速度均匀加速行驶，到达终点后停下。问以下哪个图能准确描述甲乙各自到达终点前，两车之间的距离与时间的关系(横轴为时间，纵轴为直线距离)?

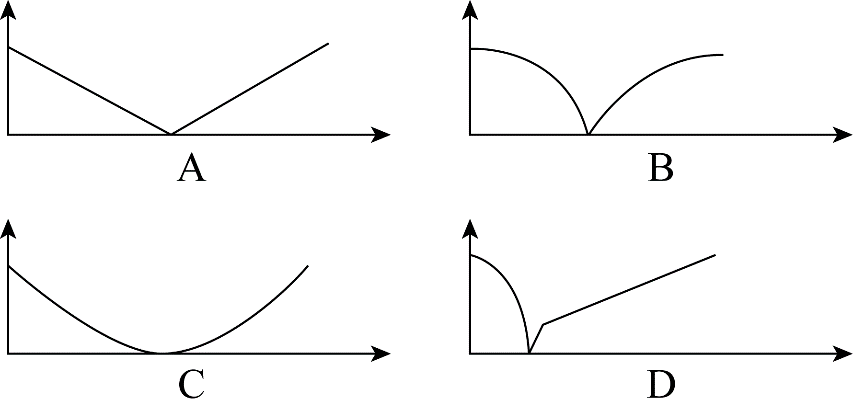
本题中出现了加速度的概念，1米/秒²的加速度表示每过1秒，速度会增加1米/秒。相遇前，两车之间的距离=100-(S甲+S乙)=100-2t-(0+t²)=100-2t-t²，随着乙车速度的逐渐增加，两车间距离减少的越来越快，所以开始阶段应该为快速下降的曲线，排除A、C选项。乙车加速度为1米/秒²，很显然乙车全程平均速度大于甲车，乙车先到达终点并停下，之后，甲车继续匀速运动，所以乙车停下后两车距离应该线性增加，排除B选项。因此选择D选项。

总之，匀加速运动类的行程问题一般都难度适中，只要在复习时理解清楚基本的运动模式，做一些典型题目，考试时完全可以轻松应对。希望通过这个讲解，能帮助大家在求解这类题目时，思路清晰，求解迅速。

相关内容推荐：