2022公务员行测备考干货：数量关系之比例法

• 资料分析题型
• 资料分析公式
• 数资易错点
• 数量关系公式
• 常识百年党史
• 全年时政热点

*资料包涵盖但不限于以上内容

扫码领福利

保存小程序码至
手机进行扫码

数量关系解题过程中有五大解题技巧：代入排除法、方程法、赋值法、枚举归纳法和比例法。这篇文章，小编好好给大家梳理一下比例法。

比例法相对代入排除法和方程法而言，对于广大考生来说，这是一种接受度较低的方法。很多考生宁愿用方程大量计算，也不愿意用比例法解题。究其原因，是因为考生对于比例法的本质理解不深，因此小编给大家系统总结一下，什么时候适合用比例法。

首先，什么是比例法?其实比例法更多针对的是三量关系中有一个定量，研究剩余两个变量的正比和反比关系。如：路程=速度×时间中，当路程一定时，速度和时间成反比关系;时间一定时，路程和速度成正比;速度一定时，路程和时间成等比。类似的三量关系还有：工作总量=效率×时间;总利润=单利润×数量……

其次，比例法应该如何使用?比例法常出现在行程问题和工程问题，需要考生们养成一个习惯，如看到路程一定，有速度之比，马上想到时间等于速度的反比建立等量关系，如下面一道例题：

【例1】(2019浙江)小王从单位开车去省城，如果他把车速提高20%，可以比原定时间提前15分钟到达;如果按原速度行驶30千米后再将车速提高到25%，也比原定时间提前15分钟到达。问小王单位距离省城多少千米?

A.60

B.120

C.180

D.240

【答案】C

【解析】第一步，本题考查行程问题，用比例法解题。

第二步，设原速度为v，由车速提高20%，可知，时间相差1份，提前了15分钟，则t=90，=75;假设全程提速25%，可知，则=72，而实际用时75分钟，故按原速度行驶30千米比提速25%后多用75-72=3(分钟)，根据比例，按原速度需用时15分钟，故原速度为30÷15=2。

第三步，按原速度行驶全程需用时90分钟，故总路程为2×90=180(千米)。

因此，选择C选项。

【本题结束】

除了行程问题，几何问题中也有部分真题偏爱用比例法。如：三角形面积=底×高÷2，当底相同，面积之比等于高之比，如以下例题：

【例2】(2019江苏)某民营企业新建一个四边形的厂区，按对角线将整个厂区分为四个功能区，如图所示。已知生产、仓储和营销三个功能区的面积分别为26亩、18亩和13亩，若保留休闲区的12亩天然小湖泊，则休闲区可利用的陆地面积是：

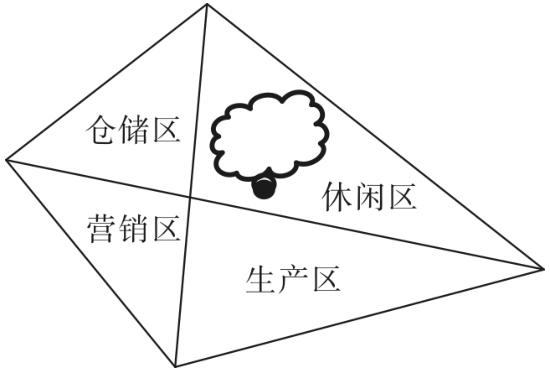
A.36亩

B.26亩

C.24亩

D.23亩

【答案】C

【解析】第一步，本题考查几何问题，属于平面几何类，用几何性质解题。

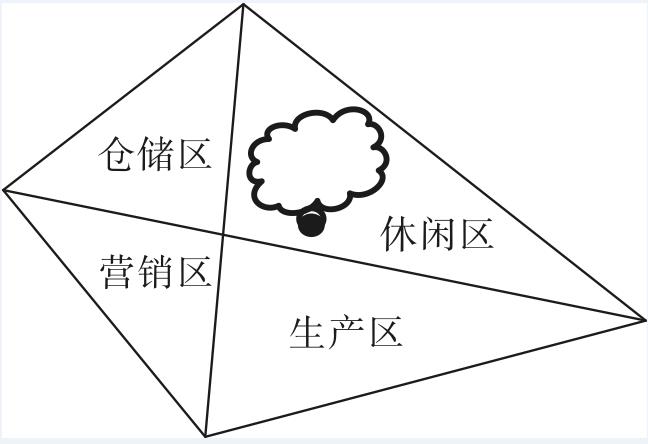
第二步,仓储区与营销区为两个等底的三角形(公用同一边)，两者面积之比为18∶13，则仓储区与营销区高之比为18：13;同理休闲区与生产区底边相同，高之比也为18：13，故面积之比也为18：13，生产区面积为26亩，则休闲区面积为26×=36(亩)。

第三步，休闲区可利用的陆地面积为36-12=24(亩)。

因此，选择C选项。

【本题结束】

比例法对于很多三量问题来说，是一种相对简便的方法，但是需要广大考生多加练习，才熟练运用，因此小编推荐以下这本书，帮助广大考生提高做题速度和正确率。

相关内容推荐：