2022省考行测最值问题解题方法及技巧

• 资料分析题型
• 资料分析公式
• 数资易错点
• 数量关系公式
• 常识百年党史
• 全年时政热点

*资料包涵盖但不限于以上内容

扫码领福利

保存小程序码至
手机进行扫码

数量关系问题在公考的成绩中决定了总成绩的最高水准，因此在考试中我们需要具备识别简单题型的能力，今天就来探讨一下在数量关系问题中的简单技巧类题型——最值问题，最值问题在考试过程中只需识别好题型，再加以一系列的技巧，这类题型是相对较简单的。

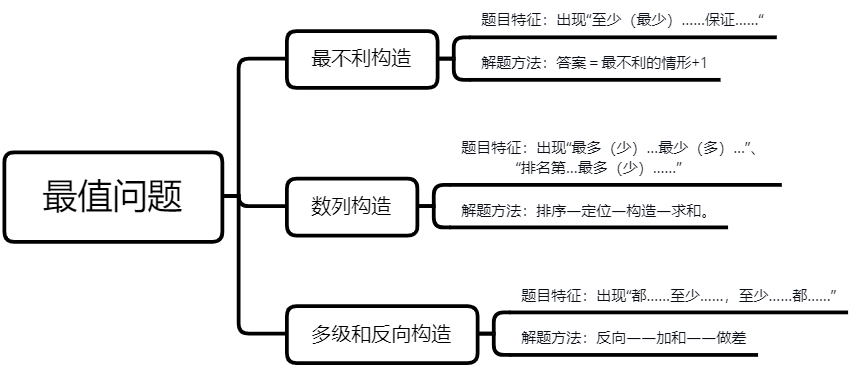
一，最不利构造

当题干中出现“至少(最少)……保证……”时，这类题型属于典型的最不利构造，在这类题型中，我们的解题方法为“最不利的情形+1”，就可以得到这类题型的最终答案。

【例一】箱子里有大小相同的3种颜色玻璃珠各若干颗，每次从中摸出3颗为一组，问至少要摸出多少组，才能保证至少有2组玻璃珠的颜色组合是一样的?

A.9B.10

C.11D.12

E.13F.14

G.16H.18

【答案】C

【解析】第一步，本题考查最值问题中的最不利构造问题，用枚举法和构造法解题。

第二步，每次摸出3颗玻璃珠，可能的颜色情况如下：

①3颗颜色都一样：有(种)可能;

②3颗中有两颗颜色一样：有(种)可能;

③3颗颜色各不相同：只有(种)可能。

综上，所有颜色的组合有3+6+1=10(种)。

第三步，最多挑出10组各不相同的颜色组合，即最不利情形为10组。在此基础上再挑一组，一定会与10组中某一组重复，即至少要摸出10+1=11(组)。

因此，选择C选项。

解法二：

第一步，本题考查最值问题中的最不利构造问题，用插板法和构造法解题。

第二步，从3种颜色玻璃珠摸出3颗球相当于将三个完全相同的玻璃珠分给3种颜色，每种颜色至少分0个，插板法(种)。

第三步，至少摸出10+1=11(组)。

因此，选择C选项。

二，数列构造

当题目中出现“最多(少)…最少(多)…”、或者“排名第…最多(少)……”时，这类题型属于数列构造，在数列构造中只需要将题目进行分解，再按照解题方法：“排序—定位—构造—求和“即可求解。

【例二】企业今年从全国6所知名大学招聘了500名应届生，从其中任意2所大学招聘的应届生数量均不相同。其中从A大学招聘的应届生数量最少且正好为B大学的一半。从B大学招聘的应届生数量为6所大学中最多的，则该企业今年从A大学至少招聘了多少名应届生?

A.48

B.47

C.46

D.45

【答案】B

【解析】第一步，本题考查最值问题，属于数列构造类，用构造法解题。第二步，设A大学招聘应届生x名，则B大学招聘应届生2x名，要想使A大学招聘应届生的人数尽可能少，那么其余大学招聘的应届生应尽可能多，构造如下表：第三步，可列方程：2x+2x-1+2x-2+2x-3+2x-4+x=500，解得，即A大学至少招聘了47名应届生。因此，选择B选项。

三，多级和反向构造

当题目中出现“都……至少……，至少……都……”时属于多级和反向构造题型，在这类题中，直接正向求解有些繁琐，因此我们可以利用反向求解，从而用总数减掉反向即为正确答案，因此，在这类题中的解题方法为：反向——加和——做差。

【例三】有100名员工去年和今年均参加考核，考核结果分为优、良、中、差四个等次。今年考核结果为优的人数是去年的1.2倍。今年考核结果为良及以下的人员占比比去年低15个百分点。问两年考核结果均为优的人数至少为多少人?

A.55

B.65

C.75

D.85

【答案】B

【解析】第一步，本题考查最值问题，属于多级和反向构造。第二步，今年考核人数为良及以下的占比降低了15个百分点，则考核结果为优的提高了15个百分点，两年的总人数均为100，即今年考核结果为优的增加了100×15%=15(人)。第三步，考核结果为优的人数是去年的1.2倍，赋值份数：5份→6份，每一份是15人，则去年人数是5×15=75，今年人数是6×15=90。第四步，两年均为优的人数至少为90+75-100=65(人)。因此，选择B选项。

相关内容推荐：