2022年省考行测数量关系等差数列你必须掌握的公式

• 资料分析题型
• 资料分析公式
• 数资易错点
• 数量关系公式
• 常识百年党史
• 全年时政热点

*资料包涵盖但不限于以上内容

扫码领福利

保存小程序码至
手机进行扫码

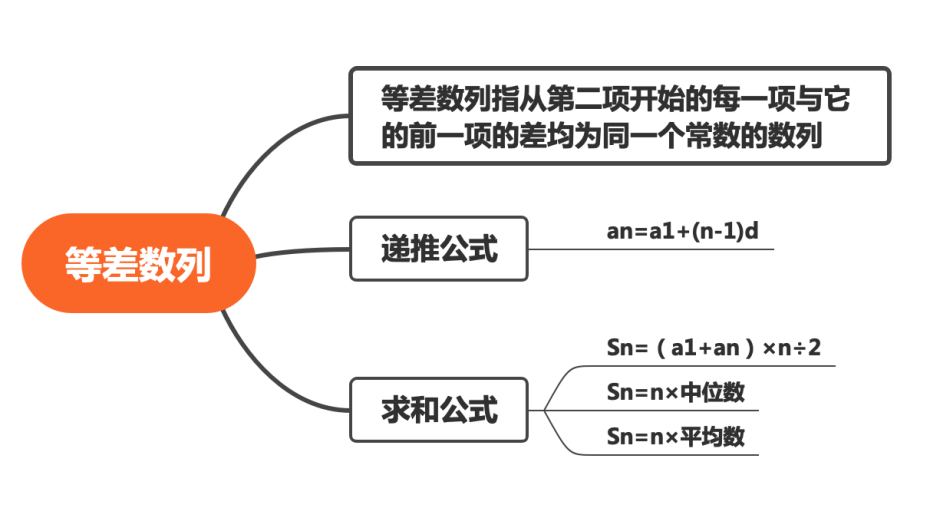
数列问题属于数量关系中初等数学问题的范畴，包含等差数列和等比数列两个部分。其中，等差数列在数量关系中考查较多。等差数列就是指从第二项开始的每一项与它的前一项的差均为同一个常数的数列。比如1，3，5，7，9……就是一个公差为2的等差数列。考试中等差数列的题目会涉及递推和求和问题，今天小编就教给小伙伴们等差数列特定公式的解题技巧。

首先，我们来看一下等差数列的递推公式。已知首项a1和公差d，求第n项an，则an=a1+(n-1)d。比如：小王在期末考试中取得了95分，是班级的第一名，他比第二名高3分，且前四名的成绩呈等差数列，那么第四名的成绩为多少呢?此问题的目的是求第四名的成绩即求等差数列的第4项，根据题意可知，首项a1=95，d=-3，则a4=95+(4-1)×(-3)=86，则第四名得86分。

学会了等差数列的递推公式，前方马上进入重难点部分即等差数列的求和公式，大家拿出小本本赶紧记下来!

我们原来学过的等差数列求和公式为false，其中首项为a1，末项为an，共n项。如果爸爸、妈妈和小亮的年龄呈等差数列且依次递减，且三者的和为135岁，那么妈妈多少岁呢?根据求和公式false，得爸爸+小亮=90岁。已知爸爸和小亮共90岁，那么妈妈的年龄为135-90=45岁。这种方法我们需要套入公式先求出爸爸和小亮的年龄和，进而求出妈妈的年龄，较复杂。今天小编给大家扩展另外两个公式，这个问题就能一步解决。

Sn=n×中位数=n×平均数。回到上面的问题，爸爸、妈妈和小亮的年龄呈等差数列且依次递减，则中位数为妈妈的年龄，代入可得135=3×妈妈的年龄，那么妈妈的年龄=135÷3=45岁，此种方法能够在特定题型中快速解题。接下来我们做一道题来检验一下大家是否完全掌握。

某成衣厂对9名缝纫工进行技术评比，9名工人的得分正好成等差数列，9人的平均得分是86分，前5名工人的得分之和是460分，那么前7名工人的得分之和是多少?

A.602B.623

C.627D.631

很显然，本题是数列问题，9名工人的得分正好成等差数列，且9人的平均得分是86分，根据公式Sn=n×中位数=n×平均数，则中位数=平均数，即第5名的成绩为86分，前5名工人的得分之和是460分，前5名的平均分=第3名的成绩=460÷5=92分，根据等差数列性质。第4名成绩=(92+86)÷2=89分，则前7名工人的得分之和=7×第4名成绩=7×89=623，选B选项。

等差数列是数列问题的重要内容，递推公式和求和公式各位小伙伴们要学会灵活运用，根据不同的问法选取解题最快速的公式。数量关系模块虽然较难高，但只要掌握技巧，我们都可以将分数拿到手!

相关内容推荐：