公务员行测备考技巧之几何问题特殊解法之赋值法巧解

• 资料分析题型
• 资料分析公式
• 数资易错点
• 数量关系公式
• 常识百年党史
• 全年时政热点

*资料包涵盖但不限于以上内容

扫码领福利

保存小程序码至
手机进行扫码

2022省考备考刻不容缓，相信有大部分考生已经加入2022省考备考大军，备考不是盲目盲从，也不是想看哪看哪，想学哪学哪，而是要有目的，有针对性的备考，要不然会像无头苍蝇一样到处乱撞。希望每位备考的小伙伴都有详细的备考计划，并且积极努力的按计划执行。在大家备考的过程中一定会有较难的模块，比如行测中的数量关系部分，看到这一模块的内容，大多数人知难而退，少部分人迎难而上，我们一起来看看数量关系中的部分较难知识点-几何问题。在看到几何题时大家都头疼，不想做也不想分析，直接跳过，其实数量关系只要掌握方法，掌握技巧，还是容易做对的。

几何问题难是因为知识点多，题型复杂，做题耗时长，大部分同学就直接放弃，今天我们一起来看看用特殊解法-赋值法解决几何问题，希望学完今天内容后大家认真复习巩固，在后续备考中逐步攻克这一部分难点。几何问题可用多种方法解决：公式法、方程法、赋值法等。几何问题的公式多，需要大家花时间去记住，方程法是解决绝大多数问题的基础方法，赋值法是在一些相对比较复杂的题目或者未给具体数值的题目中适用，相对公式法和方程法来说更快捷和方便。

接下来我们通过几道例题来看看赋值法在几何问题中的运用，一起通过例题来分析赋值法在几何问题中使用的技巧。

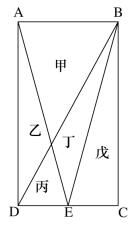
一块种植花卉的矩形土地如图所示，AD边长是AB的2倍，E为CD边的中点，甲、乙、丙、丁、戊区域分别种植白花、红花、黄花、紫花、白花。问种植白花的面积占矩形土地面积的：

A.3/4

B.2/3

C.7/12

D.1/2

解析：根据题目信息可知，本题考查几何问题，题目中未给出具体的数据，只给出对应花卉种植面积之间的关系，问题涉及对应花卉的占比，可以采用赋值法解。由图形面积关系可以赋值丙面积为1，根据“AD边长是AB的2倍，E为CD边的中点”得到AB=2DE，所以甲的面积为4(几何特性：相似图形，面积之比等于边长之比的平方)。丙和丁的底边都在DB上，顶点都为E，由于高相同，三角形面积比等于底边长之比，故得到丁的面积为2，同理可得乙的面积也为2。由于戊的面积与丙、丁面积之和相等(三角形底边长度相等，高相等)，所以戊的面积为3，矩形总面积为4+2+1+2+3=12。根据种白花的面积为4+3=7，得到白花面积的占比为。选择C选项。

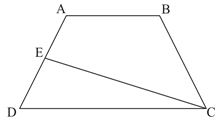
如下图，ABCD是一个梯形，E是AD的中点，直线CE把梯形分成甲、乙两部分，其面积之比为5∶2，那么上底AB与下底CD的长度之比是()。

A.2∶5

B.3∶5

C.3∶4

D.4∶7

解析：根据题目信息可知本题考查几何问题，根据题目信息本题未给出具体数值，只给出甲乙面积之比，问的是上底与下底长度之比，故可用赋值法解。根据甲、乙面积之比是5∶2，赋值甲、乙的面积分别为5和2。如下图所示：连接CA，根据E为AD“中点”知，△ACE和△CDE等底、等高，乙的面积为2，则△ACE的面积也为2，△ABC的面积为5-2=3。△ABC和△ACD等高、底不同，底分别为AB、DC，则三角形面积之比等于底边之比。选择C选项。

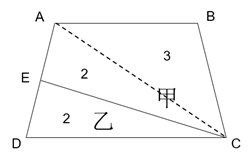
如图三角形中，A、B分别为两条边的中点，则图中阴影部分面积为三角形总面积的()。

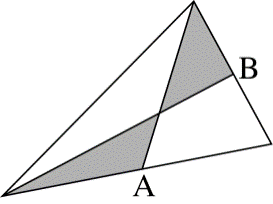
A.1/3

B.1/4

C.2/7

D.3/8

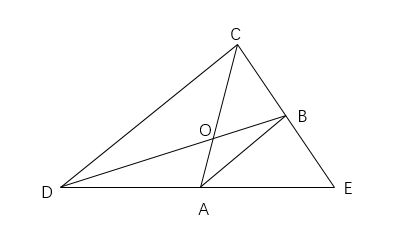
解析：根据题目信息可知本题考查几何问题。题目中未给具体数值，可考虑用赋值法解，连接AB。根据图形信息可知，如下图所示，连接AB并在图中标上对应字母，A、B分别为CE和DE两条边的中点,赋值△CDE面积为1，△BCD的面积占△CDE的，△ABD的面积占△DBE的，所以△ABD的面积占△CDE的，故△BCD的面积是△ABD的面积的2倍，则有OC∶OA=2∶1。，那么△AOD的面积占总面积的，△BOC的面积占总面积的×=，那么阴影面积(△AOD和△BOC)占总面积(△CDE)的比值为。

相关内容推荐：