2021-11-30 10:00:44 公务员考试网 
 文章来源:安徽分院
文章来源:安徽分院
容斥问题是数量关系常考题型之一,其考查频次低于经济利润问题,行程问题,几何问题,排列组合与概率等考点。虽然容斥问题的考查频次低于上述高频考点,但容斥问题一旦考查到考生经常会出错。究其原因,是因为考生不太熟悉容斥问题。在中学阶段,考生并未学习容斥问题。虽然容斥问题和集合有关系,但中学阶段并未系统型地阐述两者之间的关系,也未涉及到相关的习题。因此对大多数考生而言,容斥问题是新的考点,是以前的学习中未曾接触的考点,因此做题过程中经常出错。而三集合的容斥问题,考生更容易出错。接下来介绍三集合中常考的标准型和非标准型公式。
一 、 三集合标准型公式
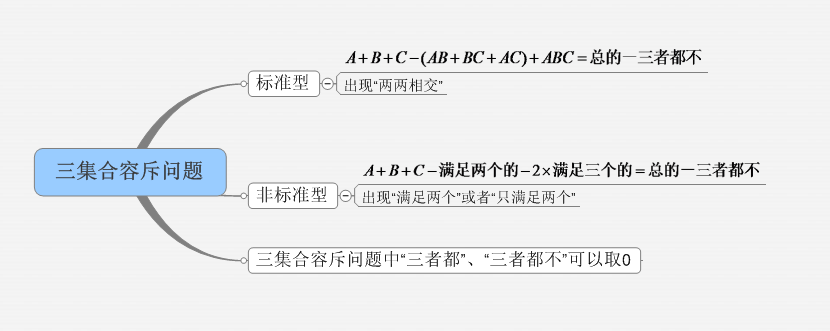
三集合标准型公式:A+B+C-(AB+BC+AC)+ABC=总的-三者都不。
关键记住左边各项及正负号,单个的是加号,两两相交的是减号,三三相交的是加号,即“+”、“-”、“+” 。
【例 1 】 针对100名旅游爱好者进行调查发现,28人喜欢泰山,30人喜欢华山,42人喜欢黄山,8人既喜欢黄山又喜欢华山,10人既喜欢泰山又喜欢黄山,5人既喜欢华山又喜欢泰山,3人喜欢这三个景点,则不喜欢这三个景点中任何一个的有多少人?
A.20 B.18
C.17 D.15
E.14 F.13
G.12 H.10
【答案】 A
【解析】 本题问的是 不喜欢 三个景点中任何一个的有多少人,即三个都不喜欢的有多少人,结合题干判定本题为三集合容斥问题 。设三个景点都不喜欢的有 x 人,根据三集合标准型公式:A+B+C-(AB+BC+AC)+ABC=总的-三者都不,得 28+30+42-(8+10+5)+3=100-x ,解得 x=20 。 因此,选择 A 选项 。
三集合标准型难度不大,直接套公式即可 。三集合容斥问题关键是判断题型,当题干中出现“三者都”或者“三者都不”时,要想到三集合的容斥问题。如果题干的已知条件完全匹配标准型公式,直接用标准型公式即可。
二 、 三集合非标准型公式
三集合非标准型公式:A+B+C-满足两个的-2×满足三个的=总的-三者都不
在三集合非标准型公式中,满足两个的只需要减掉一次,而满足三个的需要减掉两次,即三者都需要减两次。
【例 2 】某企业调查用户从网络获取信息的习惯,问卷回收率为90%,调查对象中有179人使用搜索引擎获取信息,146人从官网站获取信息,246人从社交网站获取信息,同时使用这三种方式的有115人,使用其中两种的有24人,另有52人这三种方式都不使用,问这次调查共发出了多少份问卷?
A. 310 B. 360
C. 390 D. 410
【答案】 D
【解析】 本题 题干中出现了 “三者都”、“三者都不” ,判定本题求的是 三集合容斥问题 。设本次回收的问卷数量为 x, 根据三集合非标准型公式, 得 179+146+246-24-2×115=x-52 , 解得 x= 369 。根据问卷回收率为 90%,可得发出问卷的数量为369÷90%=410(份)。 因此,选择 D 选项 。
在三集合容斥问题中,如果出现了“满足两个”或者“只满足两个”,就要考虑是否可以用三集合非标准型公式。
【例 3 】一个班级组织跑步比赛,共设100米、200米、400米三个项目。班级有50人,报名参加100米比赛的有27人,参加200米比赛的有25人,参加400米比赛的有21人。如果每人最多只能报名参加2项比赛,那么该班最多有多少人未报名参赛?
A. 11 B. 12
C. 13 D. 14
【答案】 C
【解析】 本题 题干中出现了 每人最多只能报名参加2项比赛,即出现了 “只满足两个” ,判定本题求的是 三集合容斥问题 。 根据 每人最多只能报名参加2项比赛,则报名三项比赛的人数为 0。 设参加两项 比赛 的有 x人,未报名参赛的有y人, 根据三集合非标准型公式, 得 27 + 25 + 21 - x - 0 = 50 - y,化简得y=x - 23。要使y尽量大,则x尽可能大。要使x尽可能大,则每个人尽量 参加两项比赛,参加两项比赛的人最多为( 27+25+21 ) ÷2=36.5,人数必须为整数, x 最多是36人。 解得 y = 36-23= 13 。因此,选择 C 选项 。
小结: 1.三集合标准型公式涉及的量较多,条件较为苛刻。如果出现了两两相交,考虑用标准型公式。
2.三集合容斥问题中,如果出现“满足两个”或者“只满足两个”,考虑用非标准型公式。
3.在三集合标准型和非标准型公式中, “三者都”、“三者都不”可以取 0 。

相关内容推荐:

报名条件?
岗位选择?
笔试科目?
面试方式?
......

 在线客服×
在线客服×