2022国考行测备考之几何最值理论

几何问题作为公考中常见的题型，小伙伴们一定要牢牢把握住。对于几何最值理论，小伙伴们可能还有些模糊，在这里我们就再来学习一遍几何特性中的一个特殊考点：几何最值理论。

首先我们来了解一下几何最值理论的定义：

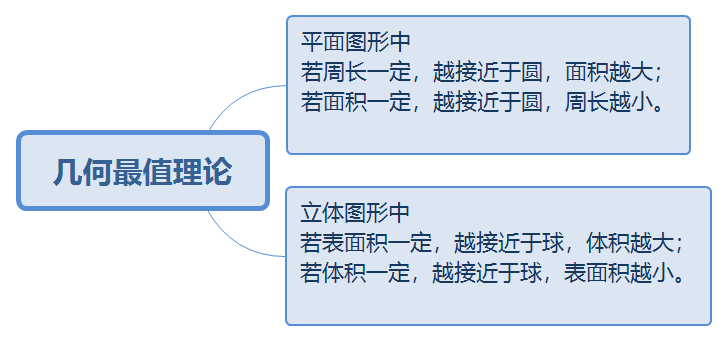
平面图形中，若周长一定，越接近于圆，面积越大;

平面图形中，若面积一定，越接近于圆，周长越小。

立体图形中，若表面积一定，越接近于球，体积越大;

立体图形中，若体积一定，越接近于球，表面积越小。

以上的四条，就是几何最值理论，当然理论是相对比较抽象的，下面就借助一些例子帮助大家形成更直观的记忆。

首先把目光聚集在平面图形中。

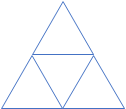
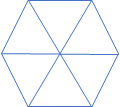
如上图所示，两个图形的周长相等，但是面积上正六边形明显要大于正三角形。因此我们容易推出：平面图形中，若周长一定，越接近于圆，面积越大。

对于立体图形而言，证明起来比较复杂，不过我们可以通过现实生活中的现象来辅助进行记忆。

上图是常见的蓄水塔，把它做成球型就是运用了几何最值理论。制作一个蓄水塔，商家就是希望它能尽可能装多的水的基础上，少使用一些材料，这样才能有效降低成本。因此做成这个形状。

当然许多小伙伴没见过蓄水塔，再说一个生活中的例子。小伙伴们小时候应该玩过吹气球的小游戏，谁先把气球吹爆就能赢得比赛。在吹气球的过程中，气球由于材质的原因有一定延展性，此时表面积是会不断增加的。但是随着气球不断变大，此时气球的表面积已经趋近于极限了，此时表面积可以近似看作不变，再继续往里面吹气，就是体积不断增加。此时我们可以看到气球由一个椭球体不断向着球体变形。这就是我们所说的立体图形中的表面积一定，越接近球，体积越大。

经过上面两个例子，相信小伙伴们对几何最值理论有了更深的体会，下面还是借助例题巩固一下。

【例题】将一个表面积为72平方米的正方体平分为两个长方体，再将这两个长方体拼成一个大长方体，则大长方体的表面积是多少平方米?

A. 56

B. 64

C. 72

D. 84

【答案】D

【解析】解法一：正方体的一个面面积为72÷6=12(平方米)将一个正方体变为长方体，表面积的变化为增加了两个侧面：12×2=24平方米，侧面的一半减少了两个，减少了12÷2×2=12平方米，因此表面积最终增加了24-12=12平方米。表面积为72+12=84平方米。

因此选择D选项。

解法二：根据几何最值理论，在立体图形中，体积一定时，越接近球，表面积越小。将一个正方体变为长方体，体积不变，而正方体比长方体更接近球，因此长方体的表面积大于正方体表面积，即长方体表面积大于72(平方米)。

因此选择D选项。

通过上面的例题，不难看出几何最值理论在一些题目中有很好的运用，希望小伙伴们都能熟练掌握。

【省考面试礼包】|【省考面试系统提升】|【省考面试图书】|【面试题库】

相关内容推荐：