2021-07-28 17:02:01 公务员考试网 
 文章来源:天津分院
文章来源:天津分院
国考行测数量考查10~15道题,一般而言,地市级10道,省部级15道。数量模块难度较大,需要策略性答题,一般来说,“做一半,蒙一半”是最佳策略,由此引出另外一个问题——“做哪一半,蒙哪一半”?毫无疑问,应该做相对简单的有把握的题型,国考数量中,相对简单且为高频考点的题型主要有基础应用题以及工程问题,今天就针对工程问题为大家进行考点剖析并进行试题预测。
工程问题是在小学阶段就学过的数学应用题,当然,行测的考题肯定比小学题目难,如果你不知道方法,不懂技巧,很难快速解出。但总的来说,工程问题只有三个要素,效率、时间、工作总量,相对而言,比其他题型简单很多。下面通过表格,为大家剖析工程问题的考点。
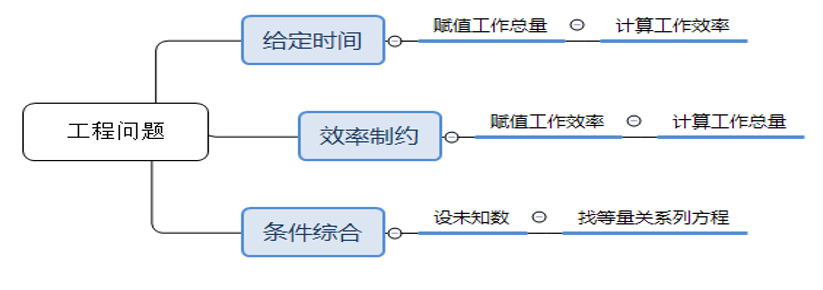
表1:从解题方法角度对工程问题进行分类
| 题型 | 特征 | 解法 |
| 给定时间型 | 给出某人或某几人完成某项工作所用的时间 | 第一步:赋值工作总量 第二步:计算工作效率 第三步:依题意进行后续计算 |
| 效率制约型 | 给出某两人或某几人做工时的效率比 | 第一步:赋值工作效率 第二步:计算工作总量 第三步:依题意进行后续计算 |
| 条件综合型 | 给出较多具体数据,一般而言,时间、效率、工作总量给出其中两个的具体数据或相关信息 | 第一步:设未知数 第二步:找等量关系列方程 第三步:解方程 第四步:依题意进行后续计算 |
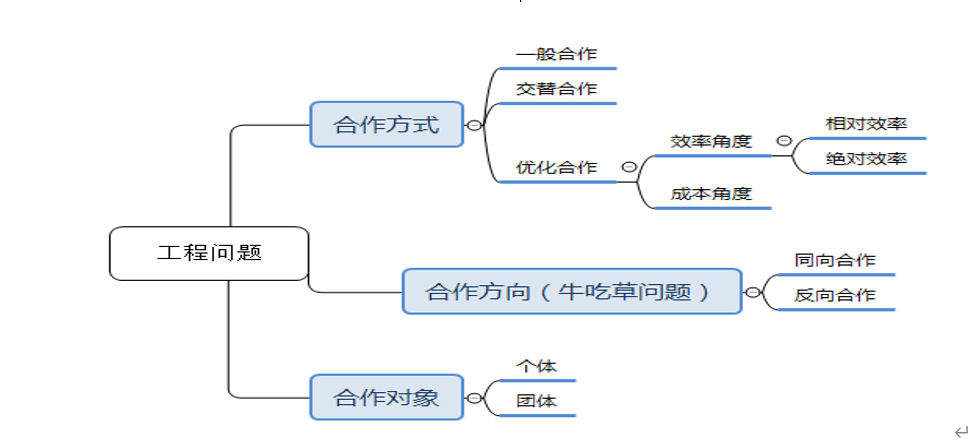
表2:从合作角度对工程问题进行分类
| 类型 | 题型 | 讲解 |
| 合作方式 | 第一种:一般合作 第二种:交替合作 第三种:优化合作 | 第一种:一般合作,即最常见题型。 第二种:交替合作,即周期性合作。 第三种:优化合作,即工程问题中求最值的题型。它又包含两种情形,一是效率角度(包括相对效率与绝对效率两种题型),二是成本角度。 |
| 合作方向 | 第一种:同向合作 第二种:反向合作 | 从合作方向角度进行命题,这类题即牛吃草问题。 |
| 合作对象 | 第一种:个体合作 第二种:团体合作 | 个体合作,例如甲、乙两人合干,即为个体合作。 团体合作,包括某个团体单独完成某工作,或几个团体合作完成某工作。 注:如何区分个体还是团体? 问:甲、乙两个公司合作,属于个体合作OR团体合作? 答:如果涉及每个公司的干活人数,即为团体合作,否则为个体合作。 |
以上是工程问题的全部考点,针对考点并结合考情,为大家预测2022年国考数量的工程问题,以下是预测试题。
【预测题目】
甲乙两人,丙丁两人均为师徒关系,正常情况下徒弟的工作效率均为师傅的80%,但若师傅不在,徒弟的工作效率会下降10%。现有A、B两项工程,工作量之比为6:7,甲乙合干A工程需要10天,丙丁合干B工程需要14天。8月1日起,四人同时开始合干两项工程,期间,甲、丙分别请假1天和3天,则竣工日期为哪一天( )
A.8月11日 B.8月12日
C.8月13日 D.8月14日
【题目解析】
本题可以归纳为给定时间型,按照解题思路,应该赋值工作总量,再计算工作效率。因为A、B两项工程的工作量之比为6:7,所以设A的工作量为540,B的工作量为630,则甲乙的效率和为540÷10=54,丙丁的效率和为630÷14=45,再根据师徒正常合干时,徒弟效率是师傅效率的80%,可推知甲的效率为30,乙的效率为24,丙的效率为25,丁的效率为20。假设四人合干需要t天完成全部工作,注意“师傅不在,徒弟的工作效率会下降10%”,则在此期间甲的工作量为30×(t-1),乙的工作量为24×(t-1)+24×90%,丙的工作量为25×(t-3),丁的工作量为20×(t-3)+3×20×90%,最后将4人的工作量加和等于工作总量即等于540+630,解得t约为12.96天,即在第13天竣工,所以竣工日期为8月13日。因此,答案选择C选项。
【预测原因】
国考工程问题的难度一般为中等,本题约为中等难度,尤其在计算方面,计算量稍大,有一定计算难度。
国考工程问题一般会出现多个对象,本题有甲乙丙丁4个对象。
国考工程问题往往需要赋值法、方程法共同使用才能解题,本题即是如此。
国考工程问题的题干一般较长,本题题干长度基本合格,实际的考题题干可能更长。
本题符合这几年国考命题的风格。
综上所述,这道预测题是很有参考价值的,大家应该以点带面,见微知著,通过这道题将工程问题融会贯通,熟练掌握。
【思维导图】

相关内容推荐:

报名条件?
岗位选择?
笔试科目?
面试方式?
......

 在线客服×
在线客服×