2021-07-01 10:36:29 公务员考试网 
 文章来源:陕西分院
文章来源:陕西分院
在我们备考公考的过程中,排列组合可谓是一个热门考点,有些题目看起来晦涩难懂,但是如果学会了一些方法之后,再看这些题目,反而觉得并没有那么难了。那么,今天呢,咱们就先看一看排列组合里面的一种较为简单的方法-隔板法,学会这个方法后很多题都迎刃而解了。
首先,隔板法是有其应用题型特征的,它经常用在相同物品分配、并且每份至少分得一个的情况。比如,将11个苹果分给4个小朋友,每人至少分得一个苹果,有多少种分配方式呢?
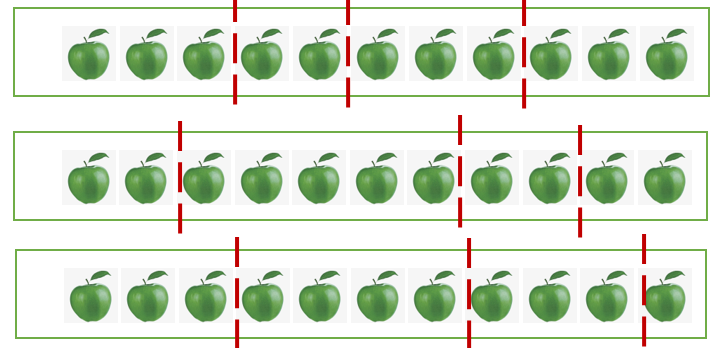
那么,到底有多少种方式呢????
其实不难发现,情况会很多,而且这样画容易出现重复。对于这类问题我们有一个公式:
将m个相同的物品,分给n个人,每人至少得一个,则共有![]() 种方式。下面我们来看一道例题。
种方式。下面我们来看一道例题。
【例 1】某城市一条道路上有4个十字路口,每个十字路口至少有一名交通协管员,现将8个协管员名额分配到这4个路口,则每个路口协管员名额的分配方案有:
A. 35种
B. 70种
C. 96种
D. 114种
[解析]
第一步,根据问题中“分配方案数”,确定该题为排列组合题。
第二步,根据题目中将8个协管员名额分配到这4个路口,满足将m个相同的物品,分给n个人,每人至少得一个,所以可以直接用隔板法公式去做。
第三步,根据公式![]() =
=![]() 。
。
因此,选择A选项。
当然,隔板法中还有一类稍微变形的题目,比如,将11个苹果分给4个人,每人至少分两个,问有多少种分配方式?
【例 2】某校召开学生会议,要将10个学生代表名额分配到某年级的4个班,若每班至少2个名额,有多少种不同分法?
A. 84种
B. 10种
C. 20种
D. 15种
[解析]
第一步,根据问题中“分配方法数”,确定该题为排列组合题。
第二步,根据题目中将10个学生代表名额分配到某年级的4个班,若每班至少2个名额,不难发现是隔板法的变形题目,可先给4个班每班分1个名额,题目就变成将6个名额分给4个班,每班至少分1个。
第三步,根据公式![]() =
=![]() 。
。
因此,选择B选项。
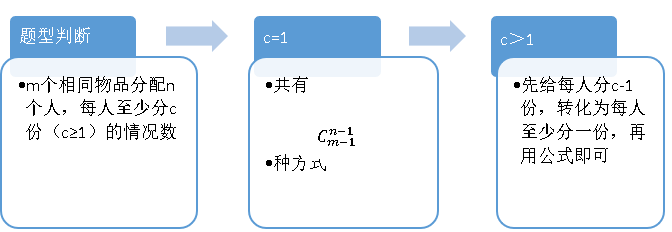
所以对于这类变形题(m个相同物品分给n个人,每人至少分c份),先给每个人分(c-1)份,再用公式计算。

| ↓↓↓↓2024年国家公务员考试相关推荐↓↓↓↓ | |||
| 公考第一课 | 2024版国考图书 | 第18版5100题 | 申论答题纸 |
| 系统提升班plus | 笔试悦享班 | 历年臻题 | APP会员年卡 |
相关内容推荐:
2024年国家公务员考试考点分布|考场设置

贴心微信客服

贴心微博客服

报名条件?
岗位选择?
笔试科目?
面试方式?
......

 在线客服×
在线客服×国家公务员考试公告 国家公务员考试大纲 国家公务员考试专业分类目录 国家公务员考试职位表 国家公务员考试报名入口 国家公务员考试报考条件 国家公务员考试报名费用 国家公务员考试报名人数 国家公务员考试报名确认 国家公务员考试准考证打印 国家公务员考试行测备考 国家公务员考试申论备考 国家公务员考试考试时间 国家公务员考试考试流程 国家公务员考试考试科目 国家公务员考试答题须知 国家公务员考试考场规则 国家公务员考试真题解析 国家公务员考试成绩查询 国家公务员考试分数线 国家公务员面试公告 国家公务员面试名单 国家公务员考试资格复审 国家公务员考试调剂名单 国家公务员面试技巧 国家公务员面试礼仪 国家公务员结构化面试 国家公务员无领导小组讨论 国家公务员考试体检考察 国家公务员考试录用公示