行测备考数量关系之排列组合-隔板法

排列组合问题是公考中的常驻题型，好多同学在学习的时候，对于基础的排列和组合已经掌握，但是对于排列组合中的各类技巧运用还不是很熟练，今天我们就排列组合中技巧之一隔板法，做一个系统的学习。

在学习隔板法的最开始，我们要明确隔板法的适用范围：运用在相同元素的分配中。那么说到相同元素，各位同学想到了哪些现实中的情况呢?我们一起来梳理一下：比如分苹果，分梨子这种情况，我们在考虑的时候，其实是不会关注哪个苹果大，哪个苹果小的，我们一般只考虑数量问题，谁分了1个苹果，谁分了2个苹果。同样的情况还有分配名额，分配人员指标等，这些情况我们都只考虑分配时候的数量多少问题。这样的情景我们就称之为相同元素的分配问题。

了解了适用范围，我们下一步就要了解一下隔板法的具体用法。通常情况，我们使用隔板法的时候还会有一个核心条件：每个分配单元至少1(N)个元素。比如分苹果，每个小朋友至少得一个苹果;分配名额，每个单位至少有一个名额。这样的时候我们怎么解题呢?把N个相同元素平均分给M个单元，则有种情况。

那么这个式子是怎么推导出来的呢，我们下面就来具体分析一下。

我们引入一个例题：老王和老李是邻居，现在有5个苹果，每个人至少拿一个苹果，有几种情况呢?

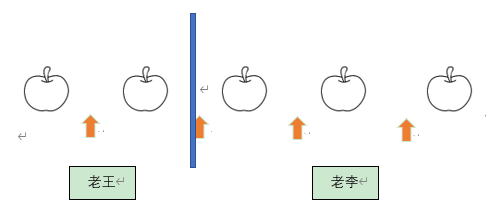
如上图所示，这就是我们使用隔板法的原理。我们要将5个苹果分给2个人，每个人至少要拿一个，那就等价于要把苹果分为两堆，一人拿一堆，那么只要在5个苹果产生的4个内部空隙中插入一个板子即可。而老王和老李只要在隔板放下后，分别拿走面前的一堆苹果，就能保证每个人至少得到一个苹果了。

所以此题使用隔板法得到的式子便是= =4。其中4代表的是5个苹果产生了4个空隙，我们要往这四个空隙种插入隔板，而1代表的是分作两堆只需要插入1个板子即可。

由此我们可以推出以下结论：N个相同元素分配给M个分配单元，所有的情况数为：

了解了隔板法的基本原理，让我们用例题来检验一下我们的学习成果。

【例1】(2020年云南)某城市一条道路上有4个十字路口，每个十字路口至少有一名交通协管员，现将8个协管员名额分配到这4个路口，则每个路口协管员名额的分配方案有：

A.35种

B.70种

C.96种

D.114种

【答案】A

【解析】观察这道题，要将8个协管员名额分配到4个路口，协管员名额属于相同元素，固这道题可以使用隔板法解题。

8个元素产生7个内部空位，分配个4个分配单元需要3个隔板，所以此题的情况数为= =35种。

结合以上所学的知识，以后再遇到分配相同元素的排列组合题的时候，同学们可以使用隔板法解题。

【省考面试礼包】|【省考面试系统提升】|【省考面试图书】|【面试题库】

相关内容推荐：