2021-06-04 15:44:45 公务员考试网 
 文章来源:云南分院
文章来源:云南分院
近几年公务员及事业单位考试中常出现一类题型即经济利润问题当中某个量增长,另一个量便减少,最后求利润最大值或收入最大值的问题。对于这类问题,绝大多数的考生都是利用一元二次方程的顶点坐标公式来进行求解,此种方法虽然也可以求出答案,但是计算过程就会稍显复杂。而对于这类题型,在这里华图教育要给大家提供一种固定的解题方法,通过此种方法可以大大简化我们的计算过程,使得计算更为简便。
【例题】某企业设计了一款工艺品,每件的成本是70元,为了合理定价,投放市场进行试销。据市场调查,销售单价是120元时,每天的销售量是100件,而销售单价每降价1元,每天就可多售出5件,但要求销售单价不得低于成本。则销售单价为多少元时,每天的销售利润最大?
A. 100元 B. 102元
C. 105元 D. 108元
【答案】C
【解析】此题要求销售单价为多少元时销售利润能达到最大值,我们先来分析:一件商品的成本是70元,销售单价是120元,所以每卖出一件商品的利润就是50元,每天的销量是100件。因为题目中说单价每降1元,销量就多卖出5件,第一步:设单价降了n次,则利润就降n元,即(50-n)元,而销量就多了5n件,即(100+5n)件,根据总利润=单件利润×销量,所以可以列出式子,总利润y=(50-n)×(100+5n)。第二步:把n前的系数x提出去,即把(100+5n)中的5提出来,这个式子变为y=5×(50-n)×(20+n)。第三步:让括号里的两数相等,即50-n=20+n,可得n=15,则销售单价为120-15=105元。因此,选择C选项。
我们利用这个题总结一下此类题的题型特征:题目中往往会出现一个量随着另外一个量的增多(减少)而减少(增多),让我们求当利润最大值或者销售收入最大值时,某个量的具体值,我们把这类题型称之为“此消彼长”类经济利润问题。接下来,我们来看一下这类题的固定解题步骤:第一步:设变化了n次,根据总收入=单件收入×销量或总利润=单件利润×销量,都可列出形如y=(a-n)×(b+xn)的式子。第二步:将n前的系数x提出去,式子化为![]() 。第三步:让括号里的两数相等,即
。第三步:让括号里的两数相等,即![]() ,求出n即可。
,求出n即可。
为了方便大家理解,这里提供一个数据处理的表格供大家参考:
| 原式 | y=(4+0.4n)×(20-n) | y=(50-n)×(100+5n) | y=(20-n)×(120+20n) |
| 提系数 | y=0.4×(10+n)×(20-n) | y=5×(50-n)×(20+n) | y=20×(20-n)×(6+n) |
| 两式相等 | 10+n=20-n | 50-n=20+n | 20-n=6+n |
| 求n | n=5 | n=15 | n=7 |
【思维导图】
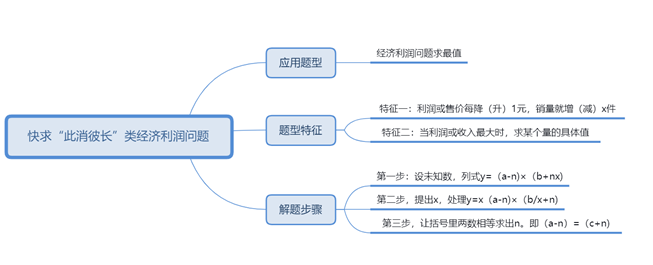

相关内容推荐:

贴心考公客服

贴心专属客服

报名条件?
岗位选择?
笔试科目?
面试方式?
......

 在线客服×
在线客服×