数量备考干货 排列组合与概率怎么做

　　纵观2021年河南省考数量关系，排列组合和概率一共有三四道题，占了数量关系部分总题量的将近1/4。之所以说是“三四道题”，是因为有一道题，虽然是求概率的，但是解题的大部分步骤用的都不是排列组合的知识，而是不定方程，题目本身的难度也不在最后一步求概率，所以只能算半道概率题吧。如果说，数量关系是广大考生在行测部分的一个痛点，那么排列组合就是痛点中的痛点。然而排列组合却是公考行测中的常考题型之一，其重要性不容忽视。

　　排列组合相对来说比较抽象，考察的是学生的逻辑思维能力，所以学习这一部分其实最根本的是理解，没有什么公式要背。我们把这一块分为两部分，包括基础的排列组合和特殊模型的排列组合，前者是重点，因为基础的排列组合学会了，特殊模型就很简单。这些基础的知识点，在华图的基础班里都会讲到，如下图所示：

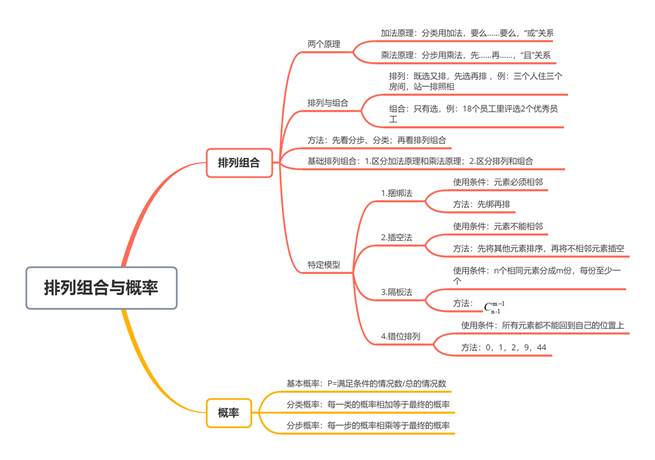
　　我们今天就来讲讲这些知识点在2021河南省考真题当中的应用。

　　【例1】 某高校开设A类选修课四门，B类选修课三门，小刘从中选取四门课程，若要求两类课程各至少选一门，则选法有：

　　A.18种 B.22种

　　C.26种 D.34种

　　【答案】D

　　例1在这15道数量关系题里，题干应该是最短的之一，理解题意不需要很长时间。这15道题里最长的题在卷子上是五六行文字再加一个图，不管题目本身是简单还是难，读懂题肯定要花不少时间，战略性放弃或者放到最后做才是比较正确的选择。而对于以上这道题，相对来说是比较基础的，应该一遍就做出来。

　　“至少选几门”，这个条件在排列组合中出现的频次极高，它是一种概括性的表述，那么你只要记住，碰到这个条件就把它所包含的所有情况先列举出来。你比如说这道题，“A类选修课四门，B类选修课三门，从中选取四门课程，若要求两类课程各至少选一门”，都可以怎么选择呢，它其实就包含了三种情况：①A类3门，B类1门;②A类2门，B类2门;③A类1门，B类3门，把这三种情况列举出来这道题就成功了一半啦。其实这第一步就是我们讲的分类，一共分成了三类情况，这一步最重要的就是按照题目的要求来分类，比如说，这道题的要求有2个，“一共选4门”和“两类课程各至少选1门”，所以你看三种情况都是，A、B两类课程数量加起来正好等于4，A、B两类课程数量都大于等于1。

　　接下来就是分别计算每一类的情况数。“①A类3门，B类1门“，这件事情操作起来就是A类先选3门，B类再选1门。第一步A类选3门，情况数是 ;第二步B类选1门，情况数是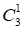。按照分步原理，每一步的情况数相乘，总的情况数是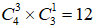。同理，②A类2门，B类2门，总的情况数是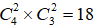;③A类1门，B类3门，总的情况数是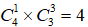。按照分类原理，把这三类的情况数相加，最终的情况数是12+18+4=34。因此，选择D。

　　【例2】 两个大人带四个孩子去坐只有六个位置的圆型旋转木马，那么两个大人不相邻的概率为：

　　A.2/5 B.3/5

　　C.1/3 D.2/3

　　【答案】B

　　这道题可以用特殊的排列组合模型来做。“元素不相邻”可以用插空法来做。两个大人不相邻，所以第一步，先排四个孩子，情况数是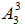(环形排列，n个元素情况数是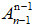);第二步，让两个大人去插空，一共有4个空，选择2个空，然后进行排列，情况数是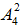;根据分步原理，把每一步的情况数相乘就是最终的情况数是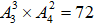。6个人坐在旋转木马是，环形排列总的情况数是。根据概率，最终的概率为。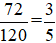

　　【例3】某公司职员小王要乘坐公司班车上班，班车到站点的时间为上午7点到8点之间，班车接人后立刻开走;小王到站点的时间为上午6点半至7点半之间。假设班车和小王到站的概率是相等(均匀分布)的，那么小王能够坐上班车的概率为：

　　A.1/8

　　B.3/4

　　C.1/2

　　D.7/8

　　【答案】D

　　班车如果7：00到达，小王只要在6：30到7：00之间到达就能赶上车;班车如果7：01到达，小王只要在6：30到7：01到达就能赶上车。时间是连续的，我们把每一时刻两者的到达情况拼在一起就是平面图形，这其实就是微积分的思想。

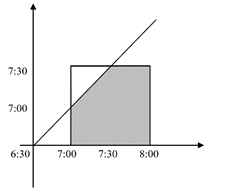
　　横坐标表示班车到达时间，纵坐标表示小王到达时间。正方形区域内的点代表所有两者到达的时间情况。在对角线以下的部分代表小王到达的时间早于班车，可以做上班车。所以阴影部分占正方形面积的比例就等于小王坐上班车的概率。假设正方形的边长是1，则最上面等腰直角三角形的边长为1/2，正方形的面积等于1，三角形的面积等于1/2×1/2×1/2=1/8，所以阴影部分面积是1-1/8=7/8，所占正方形的比例为7/8。所以能够坐上班车的概率为7/8。因此选择D。

　　这三道概率题，前两道是结合排列组合知识来考察，最后一道稍微有点难度，但是这不是第一次在公考当中出现这样的题目，华图的讲义上也有几乎一模一样的题。所以如果平时踏实学习，这三道题做出来是不成问题的。

【省考面试礼包】|【省考面试系统提升】|【省考面试图书】|【面试题库】

相关内容推荐：