行测知识点：排列组合题型如何作答

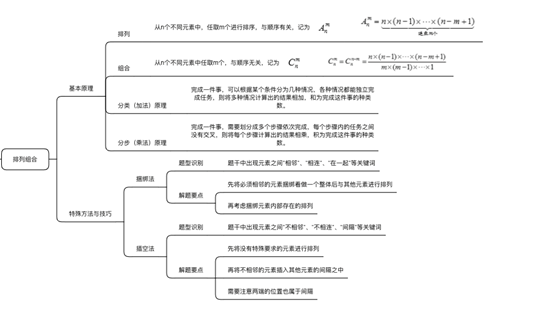
　　在行测考试中数量一直是大多数考生头疼的模块，而排列组合又是数量中的重难点，同学们在学习的时候通常不知道从哪里找突破口，并且容易被各种排列数、组合数混淆，傻傻分不清楚。首先，老师要告诉大家的是，排列组合并没有想象中的那么难，只要跟着老师认真学，这都是小意思。排列组合这个章节分成三个部分带领大家一起学习，一是知识点，二是方法技巧，三是题目练习。

　　一、知识点

　　(一)加法原理和乘法原理

　　1.加法原理：若完成一件事，可以根据某个条件分为几种情况，各种情况都能独立完成任务，则将多种情况计算出的结果相加，所得的和为完成这件事的种类数。

　　2.乘法原理：若完成一件事，需要划分成多个步骤依次完成，每个步骤内的任务之间没有交叉，则将每个步骤计算出的结果相乘，所得的积为完成这件事的种类数。

　　例：1.小明从北京到上海游玩，有3班火车，有5架次飞机可以选择，问他有多少种选择方式?

　　解：3+5=8(种)

　　2. 从少年宫到公园有2趟公交车，从公园到科技馆有3趟公交车，问小明从少年宫到公园，再去科技馆有多少种乘车方式?

　　解：2×3=6(种)

　　通过这两道题我们不难发现，我们选择乘法还是加法主要看我们完成任务是分步完成还是分类。分类用加法，分步用乘法。

　　(二)定义

　　1.排列：一般地，从n个不同元素中取出m(m≤n)个元素，按照一定的顺序排成一列，叫做从n个元素中取出m个元素的一个排列。

　　2.组合：一般地，从n个不同的元素中，任取m(m≤n)个元素为一组，叫作从n个不同元素中取出m个元素的一个组合。

　　(三)基本公式

　　1.排列公式：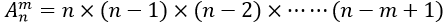 

　　这个公式看着很复杂，较难理解，我们可以通过一个小例子简化理解：

　　例：一个小组有7个人，从中选出2个人当正副组长，问有几种选择方式?

　　解：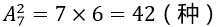

　　2.组合公式：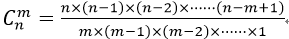

　　例：一个小组有7个人，从中选出2个人当组长(不区分正副)，问有几种方式?

　　解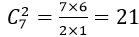：(种)

　　我想通过这两道小例子同学们应该有一些感觉了，老师给大家简单总结一下怎么区分排列与组合，需要考虑顺序为排列，无需考虑顺序为组合。

　　二、方法技巧

　　1.捆绑法：如果题目要求一部分元素必须在一起，需要先将要求在一起的部分视为一个整体，再与其他元素一起进行排列。

　　2.插空法：如果题目要求一部分元素不能在一起，则需要先排列其他主体，然后把不能在一起的元素插空到已经排列好的元素中间。

　　三、题目练习：

　　1. 某场科技论坛有5G、人工智能、区块链、大数据和云计算5个主题，每个主题有2位发言嘉宾。如果要求每个主题的嘉宾发言次序必须相邻，问共有多少种不同的发言次序?

　　A.120 B.240

　　C.1200 D.3840

　　【答案】D

　　【解析】第一步，本题考查排列组合问题，用捆绑法解题。

　　第二步，先把每个主题的2个人捆绑在一起，形成5个整体进行排列，有=120(种)排列方式，每个整体内部是2个人，有2种排列方式。故共有120×=3840(种)发言次序。

　　因此，选择D选项。

　　2. 某兴趣组有男女生各5名，他们都准备了表演节目。现在需要选出4名学生各自表演1个节目，这4人中既要有男生、也要有女生，且不能由男生连续表演节目。那么，不同的节目安排有多少种?

　　A.1200 B.2400

　　C.3000 D.3600

　　【答案】B

　　【解析】第一步，本题考查排列组合问题，属于方法技巧类的插空法。

　　第二步，根据不能由男生连续表演节目可采用插空法，先从男生和女生中选取所需要的人数，然后安排女生表演节目，最后将男生的节目插入到女生的节目之间，需要考虑顺序。有以下两种情况：

　　①1男3女，安排方式有；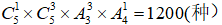

　　②2男2女，安排方式有。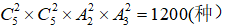

　　第三步，总安排方式为1200+1200=2400(种)。

　　因此，选择B选项。

　　同学们，经过这几道题的练习大家是不是感觉排列组合也没有大家想象中那么难呢。我们识别准题目的关键词，再套用对应的方法就能解决这类题目了。我相信只要大家好好备考，在刷题的过程中多思考多总结，排列组合这个章节对大家来说就是纸老虎，在考场上能轻松把它拿下。

【省考面试礼包】|【省考面试系统提升】|【省考面试图书】|【面试题库】

相关内容推荐：