行测知识点：善用赋值法解决工程问题

　　在日常生活中，做某一件事，制造某种产品，完成某项任务，完成某项工程等等，都要涉及到工作总量、工作效率、工作时间这三个量，探讨这三个概念之间关系的应用题，我们叫做“工程问题”。

　　除了已知其中两个量求另外一个量所用到的方程法，我们解决工程问题还可以采用赋值法，赋值法大家应该都不陌生，在我们的数学运算中运用非常广泛，几何问题、行程问题、工程问题、经济利润问题等题型都可以用到赋值法，掌握好赋值法在各类题型中应用，可以大大提高我们的解题效率。今天我们就先来看一下在工程问题中如何使用赋值法解题。

　　(2019年国考公务员考试真题(副省级)第69题)有甲、乙、丙三个工作组，已知乙组 2 天的工作量与甲、丙共同工作 1 天的工作量相同。A 工程如由甲、乙组共同工作 3 天，再由乙、丙组共同工作 7 天，正好完成。如果三组 共同完成，需要整 7 天。B 工程如丙组单独完成正好需要 10 天，问如由甲、乙组共同完成， 需要多少天?

　　A.不到 6 天 B.6 天多

　　C.7 天多 D.超过 8 天

　　【解析】第一步，本题考查工程问题，属于效率类，用赋值法解题。

　　第二步，设三者工作效率分别为甲、乙、丙，根据题意则有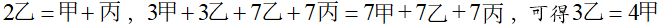：，可得3乙=4甲，我们赋值效率：甲=3，则乙=4，解得丙=5。

　　第三步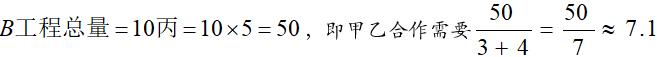， (天)，即7天多。

　　因此，选择C选项。

　　上面这道题是工程问题中已知时间以及效率之间的逻辑关系，因此我们先赋值效率，这样就可以根据基础公式：工程总量=工作时间×工作效率，求出总量，进而再求出其他量。

　　让我们再看一道只给出时间的工程问题，如何利用赋值法解决。

　　(2019年江苏公务员考试《行测》真题(C卷)第53题)一项工程由甲、乙工程队单独完成，分别需50天和80天。若甲、乙工程队合作20天后，剩余工程量由乙、丙工程队合作需12天完成，则丙工程队单独完成此项工程所需的时间是：

　　A.40天 B.45天

　　C.50天 D.60天

　　【解析】第一步，本题考查工程问题，属于给定时间类，用赋值法解题。

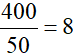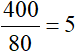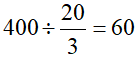　　第二步，先赋值工作总量为时间50和80的最小公倍数400，则甲的工作效率可以求出来为，乙的工作效率为。我们设丙的工作效率为X，根据题意可得，则丙单独完成所需的时间就为(天)。

　　因此，选择D选项。

　　这道题目中只给出了我们工程问题中涉及到的三个量中的其中一个量，即工作时间，那么我们就赋值工作总量为时间的公倍数，分别求出效率，将未知量转变为已知量，从而计算问题中所求的量。

　　下面我们用思维导图的形式给大家展现出来，更清晰明了，希望大家都可以掌握赋值法解决工程问题。

【省考面试礼包】|【省考面试系统提升】|【省考面试图书】|【面试题库】

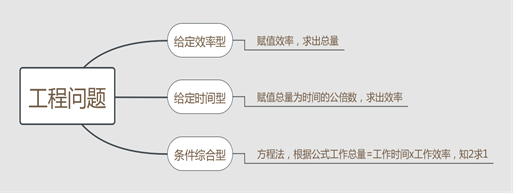
相关内容推荐：