行测备考知识点之两端出发的直线相遇问题

在行测数量关系考试的试题中，行程问题出现的概率相对比较高。主要原因我想可能是，一方面从义务教育阶段咱们就开始学习此类问题，另一方面，行程问题本身涵盖的题型就比较多，涉及运动主体也会多一些，涉及题型分类大致如下图：

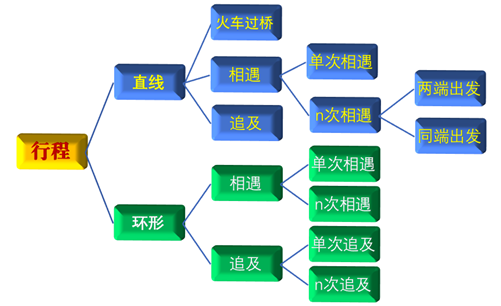
而相遇和追及问题是行程问题中永恒不变的话题，今天我们就来看看直线中两端出发的多次相遇问题在解题时，有哪些技巧。

【例1】小车和客车从甲地开往乙地，货车从乙地开往甲地，他们同时出发，货车与小车相遇20分钟后又遇客车。已知小车、货车和客车的速度分别为75千米/小时、60千米/小时和50千米/小时，则甲、乙两地的距离是：

A.205千米       B.203千米

C.201千米       D.198千米

【答案】D。华图解析：很显然，本道题属于行程问题中两端出发的直线相遇问题，因为在相遇后就不再涉及之后的过程了，所以属于单次相遇。按照相遇问题的基本公式S=(V1+V2)×T，假如我们设甲乙两地距离为S，货车和小车相遇的时间为T1，可以根据题意，列出货车与小车相遇的方程：S=(60+75)×T1，货车与客车相遇的方程为：S=，则两个方程联立解得S=198。故选择D选项。本题属于简单的单次相遇，直接按照常见的直线相遇问题的公式列方程即可解决，那么如果遇到下面这种多次相遇呢?

【例2】甲、乙两名运动员在长100米的跑道上练习短跑，甲的速度为8.5m/s，乙的速度为7.5m/s。两人同时分别从跑道的两端相向运动做折返跑，不计运动员转向及加速的时间。起跑后的1分钟内，两人共相遇了( )次。

A. 3     B. 4

C. 5     D. 6

【答案】C。华图解析：本道题涉及到的问题就比较复杂了，可以看到甲乙两人的速度和是每秒钟8.5+7.5=16m/s，100米的距离，肯定用不了1分钟两人就会第一次相遇。接下来，我们有的同学可能会这么来解题：16×60÷100=9.6次≈9次(9.6次表示还不到10次，故是9次)，但是你会发现答案中却没有9次，问题出现在哪里呢?让我们先来看看下面甲乙两人在长度为S的两端同时出发的相遇过程图：

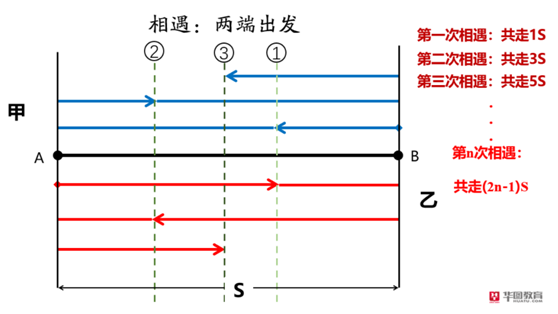
通过这张相遇过程图，我们知道，两者第一次相遇，甲乙一共走过的路程是S，而第二次相遇，甲乙一共走过的过程是3S，第三次相遇，甲乙共走过5S的总路程……由此我们总结出来，若甲乙两人第n次相遇，则他们俩走过的总路程应该为(2n-1)S，根据最原始的单次相遇公式，可以得出，在甲乙两者n次相遇时，他俩走过的总路程(2n-1)S和甲乙的速度V1、V2三者的关系是：(2n-1)S=(V1+V2)×T，此处的T是甲乙两人相遇n次所花时间。由此，我们知道，例2中两者运动过程是满足这个公式的，我们把题目中已知条件代入公式，得到：(2n-1)×100=(7.5+8.5)×60，得到n=5.3≈5次(5.3次表示还不到6次，故是5次)，故本题选择C选项。

通过上面的习题解答和过程的总结，我们得出(2n-1)S=(V1+V2)×T这样一个直线行程两端出发n次相遇中的两人速度和两地距离、及在一定时间内相遇次数关系的公式。今后再遇到此类题目，我们就可以运用这个公式去解题了，所以说，同学们在学习数量关系的过程中，要学会不断总结，找出同一类问题中共同的本质，这样才能提高学习效率，进而不断进步!

【省考面试礼包】|【省考面试系统提升】|【省考面试图书】|【面试题库】

相关内容推荐：