行测干货分享：掌握这7类搞定排列组合与概率问题

排列组合与概率问题是数学运算中常考的重难点。很多考生对这一模块知识点比较陌生，觉得这一模块抽象，不知怎么准备，本文详细给大家介绍排列组合与概率常考知识点。

当符合条件的情况比较少我们可以通过枚举的方法来解决问题，比如2个老师在3个房间里任选两间住进去，要求每人住1间共6种情况;但是如果符合条件的情况比较多，如5个老师在10个房间里任选5间住进去，每人住1间。这时再用一一枚举的方法，考场上时间是不允许的。所以我们采用排列组合来计数。它是一种科学的计数工具，既然是计数那就会涉及到加、减、乘、除。

排列组合里用的比较多的是加法和乘法。分类用加法、分步用乘法。排列用“A”表示，组合用“C”表示。组合是从n个元素中选出m个符合条件的元素;排列除了要选还要对选出来的元素进行全排列，所以：

下面我们通过基础的排列组合题目来详述：

【例1】(2019年国考-第69题) 某单位要求职工参加20课时线上教育课程，包含政治理论10课时，专业技能10课时。可供选择的政治理论课共8门，每门2课时;可供选择的专业技能课共10门，其中2课时的有5门，1课时的有5门。问可选择的课程组合共有多少种?

A.5656      B.5600     C.1848       D.616

【答案】A

【解析】本题考查基础排列组合。政治理论10课时、专业技能10课时，第一步政治课任选5门，第二步选专业技能10课时可分三类①选5门2课时的②选4门2课时的，2门1课时的③选3门2课时的，4门1课时的。分步用乘法、分类用加法，可得总情况为：

故本题选A。

【例2】(2021年联考-安徽卷第24题)某高校开设A类选修课四门，B类选修课三门，小刘从中共选取四门课程，若要求两类课程各至少选一门，则选法有：

A.18种         B.22种        C.26种       D.34种

【答案】D

【解析】本题可以像例1一样去分类求解。也可以逆向思维(总情况-不符合条件的情况)，即7门课程中任选4门课程减去四门课程全是A类的情况：。

排列组合里除了基础的题型还有典型的解题技巧和方法，包括捆绑、插空、挡板法等。 捆绑法：如果题目要求一部分元素必须在一起，需要先将要求在一起的部分视为一个整体，再与其他元素一起进行排列(注意：捆绑内部是否有顺序区别);插空法：如果题目要求一部分元素不能在一起，则需要先排列其他主体，然后把不能在一起的元素插空到已经排列好的元素中间(注意：两端是否封闭);挡板法：n个相同的元素分成m组，要求每个组至少有1个元素，可能的种类数为。

【例3】(2020国考-第62题)扶贫干部某日需要走访村内6个贫困户甲、乙、丙、丁、戊和己。已知甲和乙的走访次序要相邻，丙要在丁之前走访，戊要在丙之前走访，己只能在第一个或最后一个走访。问走访顺序有多少种不同的安排方式?

A.32       B.48       C.16       D.24

【答案】C

【解析】第一步，本题考查排列组合典型技巧捆绑、插空。

第二步，先将戊、丙、丁先后顺序排好，己有两种选择，将甲乙捆绑在一起，插空到之前安排元素所形成的4个空里。甲乙内部是有顺序区别的。

第三步，总情况为2×4×2=16(种)。

故本题选C。

【例4】(2020年联考-安徽卷13题)某城市一条道路上有4个十字路口，每个十字路口至少有一名交通协管员，现将8个协管员名额分配到这4个路口，则每个路口协管员名额的分配方案有：

A. 35种         B. 70种        C. 96种         D. 114种

【答案】A

【解析】本题考查挡板法。总情况为(种)。故本题选A。

此外排列组合还经常与概率问题结合在一起考，例如：

【例5】(2012年国考-第70题)有5 对夫妇参加一场婚宴，他们被安排在一张10 个座位的圆桌就餐，但是婚礼操办者并不知道他们彼此之间的关系，只是随机安排座位。问5 对夫妇恰好都被安排在一起相邻而坐的概率是多少?

A. 在1‰到5‰之间         B. 在5‰到1%之间

C. 超过1%        D. 不超过1‰

【答案】A

【解析】本题考查概率。

方法一：用分步概率求解。假设圆桌顺时针分别为1-10号位。现在1号位上安排一个人，任选一人即可，概率为1;第二步，此人的配偶想要和其坐一起只能坐2号或10号，概率为;第三步，在剩下的8人中任选一人坐在3号位，概率为1;第四步，坐在3号位的人其配偶能坐在4号位的概率为;第五步，在剩下的6人中任选一人坐在5号位，概率为1;第六步，坐在5号位的人其配偶能坐在6号位的概率为;第七步，在剩下的4人中任选一人坐在7号位，概率为1;第八步，坐在7号位的人其配偶能坐在8号位的概率为，剩下的两个人自然为一对夫妇。所以概率为，略大于千分之二。

方法二：可用环形排列的公式求解。N个人排成一圈和N-1个人排成一列情况数相同均为种，将5对夫妇捆绑成5个整体，捆绑的内部有顺序。所以其概率为。

故本题选A。

除了环形排列，考生还需要了解错位排列相关知识点：有n个元素和n个位置，如果要求每个元素的位置与元素本身的序号都不同，则n个元素对应的排列情况分别为，D1=0种，D2=1种，D3=2种，D4=9种，D5=44种，……Dn=(n-1)×(Dn-2+Dn-1)种;此外还需要知道平均分组的题目要记得去重复。

附：排列组合与概率思维导图

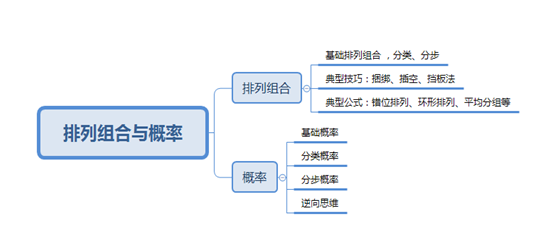
希望考生能多加练习，更多相关考试信息请及时关注华图教育官网!

【省考面试礼包】|【省考面试系统提升】|【省考面试图书】|【面试题库】

相关内容推荐：