行测备考干货：分步概率之某两个元素在一起题型解析

　　很多人提起数量关系就会说没时间，反正也不会，自己内心已经给自己划了个框;提起排列组合与概率更是觉得有点难，告诉自己我是文科生，以前基本没学过。实际上，它并没有我们想象中的那么难。

　　【2018国考】某单位的会议室有5排共40个座位，每排座位数相同。小张和小李随机入座，则他们坐在同一排的概率：

　　A.高于20%

　　B.正好为20%

　　C.高于15%但低于20%

　　D.不高于15%

　　【解析】第一步，本题考查基本概率，用分步概率法解题。

　　第二步，总情况数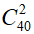,符合要求的情况数即五排中选一排，再从该排中选择两个座位，即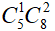，则他们坐在同一排的概率为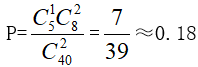，由此选择C选项。

　　此时可能有同学会想，这是常规思维，但是我就是想不到，接下来，给大家介绍另外一种思路。

　　在这道题目中，要求小张和小李坐在同一排，总共有40个座位，分为5排，每排8个座位，此时，我们可以先让两人中其中一人先随机入座，以小张为例，他就有40个座位可以坐，同时，随机入座小李就有39个座位可以选;而题干要求两人在同一排，小张入座40个座位选择，去坐后就确定了是哪一排，小李就只能从剩余7个座位中选择，因此他们坐在同一排的概率为。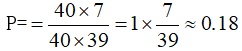

　　由此不难发现，对于概率问题要求两个人坐座位，站队在同一排的问题，我们可以先考虑第一个人，他的概率是1，实际答案为第二人的概率。

　　【2018年陕西】胜利小学的225名同学与红旗小学的256名同学一起春游，将两所小学的同学混合在一起，随机组合，重新组织队伍，要求每队人数相同且队伍数尽可能少，那么胜利小学的张华与红旗小学的张明出现在同一队伍的概率约为：

　　A.1.5% B.2.5%

　　C.3.5% D.4.5%

　　E.5.5% F.6.5%

　　G.7.5% H.8.5%

　　【解析】第一步，本题考查基本概率，用分步概率法解题。

　　第二步，两所小学的同学混合之后的总人数为225+256=481(人)，要使每队人数相等，将481进行因式分解，得到481=37×13，要使队伍数尽可能少，则一共有13支队伍，每队37人。让张华先选择一个队伍，此时还剩481-1=480(个)位置可供张明选择，每队37人，张华已经占了一个位置，队伍中还剩37-1=36(个)位置满足与张华一队。

　　第三步，那么张华和张明出现在同一支队伍的概率为：。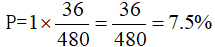

　　因此，选择G选项。

　　【2019年云南】某学校举行迎新篝火晚会，100名新生随机围坐在篝火四周。其中，小张与小李是同桌，他俩坐在一起的概率为：

　　 
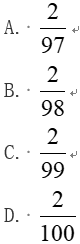
      【解析】第一步，本题考查基本概率，用分步概率法解题。

　　第二步，100名新生随机围坐在篝火四周，即会产生100个座位，假定小张选择任一个位置坐下，则小李只能从剩余的99个位置中选择坐下，与小张坐在一起的情况有两种，即坐小张的左右两侧。

　　第三步，故所求概率为。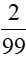

　　因此，选择C选项。

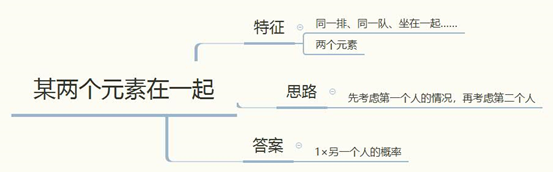
　　通过上述几道例题的讲解，相信大家对某两个元素在一起求概率问题已经有所了解，希望大家可以掌握此类题目的特征以及解题方法，在做题以及考试的过程中可以加以应用。最后我们再讲此类题目总结。

【省考面试礼包】|【省考面试系统提升】|【省考面试图书】|【面试题库】

相关内容推荐：