2021年福建省公务员行测：数学运算之排列组合习题讲解

【例题1】 自然数12321，90009，41014 ……有一个共同特征：它们倒过来写还是原来的数，那么具有这种“特征”的五位偶数有( )个。

A.400

B.500

C.900

D.40000

【例题解析】

本题就是一道典型乘法原理题目由于所求是偶数，同时，第一位也不能是0，所以个位只有四种可能2、4、6、8十位有十种可能1、2、3……9、0百位有十种可能1、2、3……9、0所以一共有4×10×10=400种可能

故应选择A选项。

【重点提示】任何数字的首位均不能为“0”。

【例题2】(2008国考第57题)一张节目表上有3个节目，如果保持这三个节目的相对顺序不变，再添加进去两个新节目，有多少种安排方法?

A.20

B.12

C.6

D.4

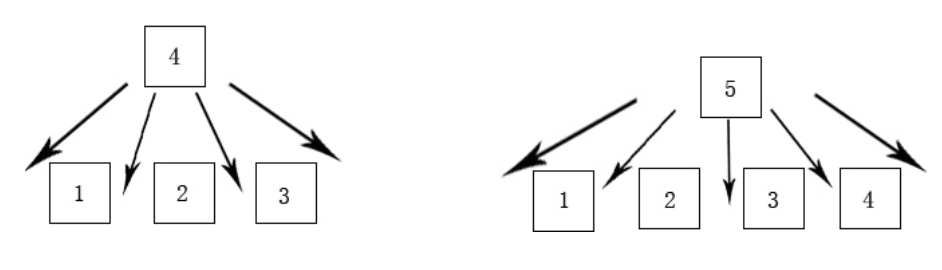
【例题解析】第一个新节目加入有4种选择。第一个新节目安排进去之后，为四个节目。那么第五个节目添加进去的时候有5种选择，所以添加方法总共有4x5=20种，故应选择A选项。

【例题3】有十张币值分别为1分、2分、5分、1角、2角、5角、1元、2元、5元、10元的人民币，能组成多少种不同的币值?

A.1021

B.1022

C.1023

D.1024

【例题解析】分币一共3种，可有8种取法1、2、5、1+2、1+5、2+5、全取和全不取同理角币也是8种取法，元币有16种取法。这样共有8×8×16-1=1023种取法，减一种是因为不能都不取，0不算一种币值。故应选择C选项。

【思路点拨】将十个币种按“元、角、分”分类考虑，结合乘法原理的应用，可以有效简化答题步骤。

【例题4】(2005年国家考试一卷48题)从1，2，3，4，5，6，7，8，9中任意选出三个数，使它们的和为偶数，则共有( )种不同的选法。

A.40

B.41

C.44

D.46

【例题解析】欲使任意3数的和为偶，则只有两种情况，①三个数都是偶数 ②三个数中，一个为偶数，两个为奇数。

1—9中有4个偶数，2、4、6、8，他们三个一组，共是4种可能

1—9中有5个奇数，1、3、5、7、9，他们两两一组，共有10种可能。

三个数都是偶数的情况有4种可能;一个为偶数，两个为奇数有10×4=40种可能。共有4+40=44种不同选法，故应选择C选项。

【例题5】(2007年浙江第16题)同时扔出A、B两颗骰子(其六个面上的数字都为1,2,3,4,5,6)问两个骰子出现的数字的积为偶的情形有几种?

A、27种

B、24种

C、32种

D、54种

【例题解析】两个骰子出现的数字的积的情况共有6×6=36种只有两个骰子同时出现奇数时，它们的积才是奇数，共有3×3=9 那么出现偶数的情况为：36-9=27

故应选择A选项。

【重点提示】此题采用剔除的办法，有效地简化了答题步骤。

【省考面试礼包】|【省考面试系统提升】|【省考面试图书】|【面试题库】

相关内容推荐：