2020重庆市考行测笔试之倍数特性试题

• 资料分析题型
• 资料分析公式
• 数资易错点
• 数量关系公式
• 常识百年党史
• 全年时政热点

*资料包涵盖但不限于以上内容

扫码领福利

保存小程序码至
手机进行扫码

在行测备考中经常会出现一些正面去解非常的麻烦，而利用倍数特性就非常简单的题目，很多学生遇到这类题目会感到束手无策，那么倍数特性类的题目有什么特征呢?

在题目中出现比例、分数、小数、百分数的时候，我们就要优先想到这是倍数特性类的题目了。另一方面如果题目里出现了平均数、余数类的意思这类题目其实也是考察的倍数特性。那么倍数特性的核心是什么呢?

若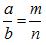(m、n互质)，则a是m的倍数，b是n的倍数，a±b是m±n的倍数。这个式子是倍数特性的核心公式。那么怎么去应用倍数特性呢?接下来，我们从几个例题中去体会一下。

【例1】 甲工厂每天生产的零件数比乙工厂的1.5倍还多40个，乙工厂每天生产的零件数比甲工厂的一半多20个。则两个工厂每天共能生产多少个零件?

A. 400 B. 420

C. 440 D. 460

解法一：传统的方法，我们利用方程法来解答。

设甲、乙每天生产的零件数分别为x个、y个，可得方程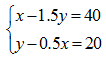，解得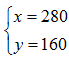，两个工厂每天“共”生产x+y=440个。因此，选择C选项。

解法二：利用倍数特性来解答

由乙每天生产的零件比甲的一半多20，可得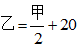。两个厂每天共能生产的零件个数为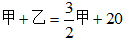，故所求值减去20后一定是3的倍数，只有C选项满足。因此，选择C选项。

【例2】某企业共有职工100多人，其中，生产人员与非生产人员的人数之比为4∶5，而研发与非研发人员的人数之比为3∶5。已知生产人员不能同时担任研发人员，则该企业不在生产和研发两类岗位上的职工有多少人?

A. 20

B. 30

C. 24

D. 26

思路剖析：这道题的难点就在于这个企业有多少员工。我们用传统的方法很难算出来。细看题目可以发现题干中出现了两组比例，是倍数特性类的题目。

解法：根据生产与非生产人员的人数“之比”为4:5，得总人数为9的倍数;同理，由“之比”为3:5，得总人数为8的倍数，因此总人数为72的倍数;由“共”有职工100多人可知，总人数应为72x2=144人。那么，生产人员为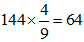人，研发人员为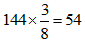人，由生产人员“不能”同时担任研发人员，可知不在生产和研发岗位的人数有144-64-54=26人。因此，选择D选项。

相关内容推荐：