2018年福建公务员考试行测技巧：工程问题巧解题

• 资料分析题型
• 资料分析公式
• 数资易错点
• 数量关系公式
• 常识百年党史
• 全年时政热点

*资料包涵盖但不限于以上内容

扫码领福利

保存小程序码至
手机进行扫码

一般情况下多者合作问题的解题方法是比例法与特值法相结合解题，下面华图教育以三道例题为例来详细讲解如何应用。

1.特值法

在很多工程问题中题中所给的数据均为以时间为单位的数据，因此题中还存在着很多变量，面对这种题型，我们采用特值法来解题。

1.设特值的方法如下

(1)若题中给出参与者的效率之比，则设比例系数为特值。例如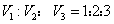，则设三者的效率分别为1.2.3来解题。

(2)若题中没有给出三者的效率比，则设工作总量为特值。注意工作总量不能设成“1”，这样列式中会出现很多分数和小数，影响做题效率和准确性，应该把工作总量设成时间条件的最小公倍数。

【例】一条公路，甲队单独去修理需要20天完成，乙队单独去修理需要30天完成。问甲乙一起修理需要多久?

A 9天 B 10天 C11天 D12天

答案D

【分析】设工作总量为20和30的最小公倍数60，则列式为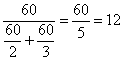天

2.结合比例法解题

【例】一批待加工的零件，甲单独做需要15小时完成，乙单独做需要10小时完成。如果两人合作，那么完成任务时乙比甲多做20个零件。这批零件共多少个?

A100 B120 C125 D200

答案A

【分析】设工作总量为30，则甲速为2，乙速为3 。两者的速度比为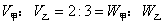。两者的工作总量之差为，对应的份数差为一份，因此一份的值为20 。比例中总做量为5份，对应的实际值为5*20=100 。

相关内容推荐：