2015辽宁公务员考试《行测》排列组合常用解题技巧

• 资料分析题型
• 资料分析公式
• 数资易错点
• 数量关系公式
• 常识百年党史
• 全年时政热点

*资料包涵盖但不限于以上内容

扫码领福利

保存小程序码至
手机进行扫码

　　在行测考试中，排列组合问题通常联系实际，生动有趣，但题型多样，思路灵活，不易掌握。下面华图教育将重点讲解排列组合中的三种方法，帮助大家有效备考。

　　1、捆绑法

　　要求某几个元素必须排在一起的问题，可以用捆绑法来解决。将需要相邻的元素合并为一个元素，再与其它元素一起排列，同时要注意合并元素内部也可以作排列。

　　2、插空法

　　对于某两个元素或者几个元素要求不相邻的问题，可以用插空法。即先排好没有限制条件的元素，然后将有限制条件的元素按要求插入排好元素的空档之中即可。

　　3、“至少”问题逆向操作法

　　当考生遇到排列组合或者概率题目中的“至少……就(才)能……”问题时，可以采取“反其道而行之”的办法，先找到问题的反面是什么情况，再利用总的情况数减去这类问题的反面情况数，其实就是题干所要求的情况。核心公式：某条件成立的情况数=总数一该条件不成立的情况数。如：从4台甲型和5台乙型电视机中任取出3台，其中至少要甲型和乙型电视机各一台，则不同取法共有多少种?

　　分析1：逆向思考，至少各一台的反面就是分别只取一种型号，不取另一种型号的电视机，故不同的取法共有

　　种。

　　分析2：正向思考，至少要甲型和乙型电视机各一台可分两种情况：甲型1台乙型2台;甲型2台乙型1台;故不同的取法有

　　种。

　　【例1】甲乙两人从5项健身项目中各选2项，则甲乙所选的健身项目中至少有1项不相同的选法共有( )。

　　A.36种　　B.81种　　C.90种　　D.100种

　　【答案】C

　　【解析】题干中出现至少有1项这样表述，逆向思考，其对立面即为甲乙两个人选的项目都相同，即

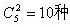
　　，那甲乙两人在无任何条件下的选取总数为

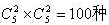
　　，某条件成立的情况数=总数一该条件不成立的情况数，即为100一10=90种，选C。

　　【例2】有8本不同的书，其中数学书3本，外语书2本，其它学科书3本。若将这些书排成一列放在书架上，让数学书排在一起，外语书也恰好排在一起的排法共有多少种?

　　A.1024种　　 B.1440种　 　C.2048种　　D.640种

　　【答案】B

　　【解析】把3本数学书“捆绑”在一起看成一本大书，2本外语书也“捆绑”在一起看成一本大书，与其它3本书一起看作5个元素，共有A55=120种排法;3本数学书有A33=6种排法，2本外语书有2种排法;根据分步乘法原理共有120×6×2=1440排法，选B。

　　【例3】一张节目表上原有3个节目，如果保持这3个节目的相对顺序不变，再添加进去2个新节目，有多少种安排方法?

　　A.20 B.12 C.6 D.4

　　【答案】A。

　　【解析】根据题意将2个节目插入3个节目当中，注意到第一个节目之前以及最后一个节目之后还可加入，因此插入第一个新节目时可有4种选择，等插入这个节目之后，再插入第二个新节目时可有5种选择。因此总共可安排的播放方案有4×5=20种。

相关内容推荐：